6850. На катете BC
прямоугольного треугольника ABC
с прямым углом при вершине C
и углом 30^{\circ}
при вершине A
вне треугольника построен равносторонний треугольник BCD
. Прямая AD
пересекает сторону BC
в точке K
.
а) Докажите, что CK:KB=1:2
.
б) Прямая, проходящая через точку K
перпендикулярно CD
, пересекает гипотенузу AB
в точке M
. Найдите отношение AM:MB
.
Ответ. 5:1
.
Решение. а) Обозначим BC=a
. Тогда BD=CD=a
, AB=2a
, а так как \angle BCD=60^{\circ}=\angle ABC
, то CD\parallel AB
. Значит, треугольник DKC
подобен треугольнику AKB
, причём коэффициент подобия равен \frac{CD}{AB}=\frac{1}{2}
. Следовательно, \frac{CK}{KB}=\frac{1}{2}
.
б) Поскольку прямые AB
и CD
параллельны, KM\perp AB
. Из прямоугольного треугольника BMK
находим, что
MB=\frac{1}{2}BK=\frac{1}{2}\cdot\frac{2}{3}BC=\frac{1}{3}BC=\frac{1}{3}a.
Тогда
AM=AB-MB=2a-\frac{1}{3}a=\frac{5}{3}a.
Следовательно,
\frac{AM}{MB}=\frac{\frac{5}{3}a}{\frac{1}{3}a}=5.
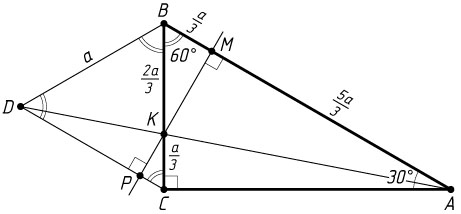
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2015
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6.25.1, с. 60
