6864. Угол B
треугольника ABC
равен 60^{\circ}
, AB\ne BC
. Окружность, вписанная в треугольник, касается его стороны AC
в точке M
.
а) Докажите, что отрезок BM
меньше трёх радиусов этой окружности.
б) Найдите синус угла BMC
, если BM
в 2,5 раза больше радиуса окружности.
Ответ. 0,65.
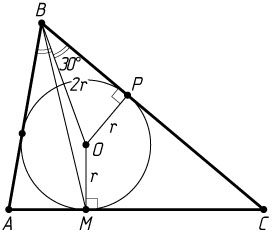
Решение. а) Пусть r
— радиус вписанной окружности треугольника ABC
, O
— её центр, P
— точка касания со стороной BC
. Поскольку BO
— биссектриса угла ABC
, угол OBP
равен 30^{\circ}
. Из прямоугольного треугольника BOP
находим, что BO=2OP=2r
. Точка O
не лежит на отрезке BM
, так как AB\ne BC
. Применив неравенство треугольника к треугольнику BOM
, получим, что
BM\lt BO+OM=2r+r=3r.
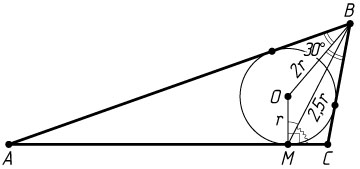
б) Предположим, что AM\gt MC
. Тогда
\angle BMC=\angle OMC-\angle OMB=90^{\circ}-\angle OMB.
По теореме косинусов
\sin\angle BMC=\sin(90^{\circ}-\angle OMB)=\cos\angle OMB=
=\frac{OM^{2}+BM^{2}-OB^{2}}{2OM\cdot BM}=\frac{r^{2}+\frac{25}{4}r^{2}-4r^{2}}{2\cdot r\cdot\frac{5}{2}r}=\frac{13}{20}=0{,}65.
Если же AM\lt MC
, аналогично получим тот же результат.
Источник: ЕГЭ. — 2016

