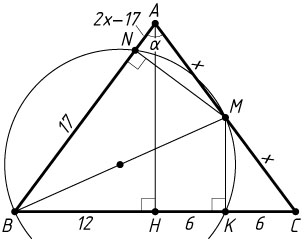
6865. Окружность, построенная на медиане BM
равнобедренного треугольника ABC
как на диаметре, пересекает основание BC
в точке K
.
а) Докажите, что отрезок BK
втрое больше отрезка CK
.
б) Пусть указанная окружность пересекает сторону AB
в точке N
. Найдите AB
, если BK=18
и BN=17
.
Ответ. 18
.
Решение. а) Пусть AH
— высота треугольника ABC
. Точка K
лежит на окружности с диаметром BM
, поэтому \angle BKM=90^{\circ}
, значит, MK\parallel AH
, а так как M
— середина AC
, то MK
— средняя линия треугольника AHC
. Тогда K
— середина CH
, следовательно,
CK=\frac{1}{2}CH=\frac{1}{2}\cdot\frac{1}{2}BC=\frac{1}{4}BC,~BK=3CK.
б) Положим AB=AC=2x
, \angle BAC=\alpha
. Тогда AM=x,~AN=2x-17
. Из прямоугольного треугольника AMN
находим, что
\cos\alpha=\frac{AN}{AM}=\frac{2x-17}{x},
а так как BC=BK+CK=18+6=24
, то по теореме косинусов
\cos\alpha=\frac{AB^{2}+AC^{2}-BC^{2}}{2AB\cdot AC}=\frac{4x^{2}+4x^{2}-24^{2}}{2\cdot2x\cdot2x}=\frac{x^{2}-72}{x^{2}}.
Из уравнения \frac{x^{2}-72}{x^{2}}=\frac{2x-17}{x}
находим, что x=8
или x=9
.
В первом случае AN=2x-17=-1
, что противоречит условию (точка N
должна лежать на отрезке AB
). Второе решение удовлетворяет условию задачи. Следовательно, AB=2x=18
.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2015
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 5.30.2, с. 51; № 11.49.1, с. 119
