6867. В треугольнике ABC
сторона BC
равна a
, высота к ней равна h
. Точка D
делит сторону BC
в отношении k
. Найдите площадь треугольника с вершинами в центрах окружностей, описанных около треугольников ABC
, ABD
и CAD
. Чему равна эта площадь, если a=4
, h=2
, k=3
?
Ответ. \frac{ka^{3}}{8(k+1)^{2}h}
; \frac{3}{4}
.
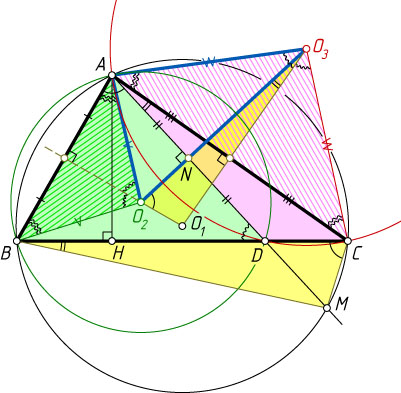
Решение. Пусть O_{1}
, O_{2}
, O_{3}
— центры окружностей, описанных около треугольников ABC
, ABD
и CAD
соответственно, M
— точка пересечения луча AD
с описанной окружностью треугольника ABC
, \frac{BD}{DC}=k
, AD=x
.
Прямые O_{1}O_{3}
, O_{1}O_{2}
и O_{2}O_{3}
— серединные перпендикуляры к отрезкам AC
, AB
и AD
соответственно, поэтому
\angle O_{1}O_{2}O_{3}=\angle BAD=\angle BCM,
\angle O_{1}O_{3}O_{2}=\angle CAM=\angle CBM.
Значит, треугольники O_{1}O_{2}O_{3}
и MCB
подобны по двум углам.
Из подобия треугольников CDM
и ADB
получаем, что \frac{MC}{AB}=\frac{CD}{AD}
, откуда
MC=AB\cdot\frac{CD}{AD}=\frac{AB\cdot\frac{a}{k+1}}{x}=\frac{AB\cdot a}{x(k+1)}.
Из подобия треугольников BDM
и ADC
получаем, что \frac{BM}{AC}=\frac{BD}{AD}
, откуда
BM=AC\cdot\frac{BD}{AD}=\frac{AC\cdot\frac{ka}{k+1}}{x}=\frac{AC\cdot ka}{x(k+1)}.
Тогда
S_{\triangle MCB}=\frac{1}{2}BM\cdot MC\sin\angle BMC=
=\frac{1}{2}\cdot\frac{AC\cdot ka}{x(k+1)}\cdot\frac{AB\cdot a}{x(k+1)}\sin(180^{\circ}-\angle BAC)=\frac{ka^{2}}{x^{2}(k+1)^{2}}\cdot\frac{1}{2}AC\cdot AB\sin\angle BAC=
=\frac{ka^{2}}{x^{2}(k+1)^{2}}S_{\triangle ABC}=\frac{ka^{2}}{x^{2}(k+1)^{2}}\cdot\frac{1}{2}ah=\frac{ka^{3}h}{2x^{2}(k+1)^{2}}.
Равнобедренные треугольники AO_{2}B
и AO_{3}C
подобны по двум сторонам и углу между ними, так как
\angle AO_{2}B=2\angle ADB=2(180^{\circ}-\angle ADC)=360^{\circ}-2\angle ADC=\angle AO_{3}C.
Тогда \angle BAO_{2}=\angle CAO_{3}
, значит,
\angle O_{2}AO_{3}=\angle O_{2}AC+\angle CAO_{3}=\angle O_{2}AC+\angle BAO_{2}=\angle BAC,
а так как из подобия равнобедренных треугольников AO_{2}B
и AO_{3}C
следует, что \frac{AO_{2}}{AO_{3}}=\frac{AB}{AC}
, то треугольники ABC
и AO_{2}O_{3}
также подобны по двум сторонам и углу между ними. Значит, если N
— середина AD
(а тогда AN
— высота треугольника AO_{2}O_{3}
) и AH
— высота треугольника ABC
, то
\frac{O_{2}O_{3}}{BC}=\frac{AN}{AH}=\frac{x}{2h},
а так как \frac{O_{2}O_{3}}{BC}
— коэффициент подобия треугольников O_{1}O_{2}O_{3}
и MCB
, то
S_{\triangle O_{1}O_{2}O_{3}}=\left(\frac{x}{2h}\right)^{2}\cdot S_{\triangle MCB}=\frac{x^{2}}{4h^{2}}\cdot\frac{ka^{3}h}{2x^{2}(k+1)^{2}}=\frac{ka^{3}}{8(k+1)^{2}h}.
Если a=4
, h=2
, k=3
, то S_{\triangle O_{1}O_{2}O_{3}}=\frac{3}{4}
.
Источник: Соросовская олимпиада. — 1994, I, 1-й тур, 10 класс
