6868. Квадрат ABCD
вписан в окружность. Хорда MK
этой окружности проходит через середины сторон BC
и CD
.
а) Докажите, что треугольник AMK
равносторонний.
б) Найдите площадь этого треугольника, если сторона квадрата равна 1.
Ответ. \frac{3\sqrt{3}}{8}
.
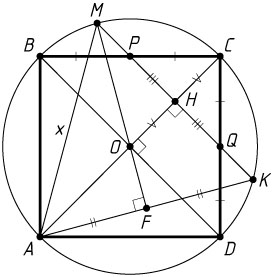
Решение. а) Пусть O
— центр окружности, а прямая MK
пересекает стороны BC
и CD
квадрата в точках P
и Q
соответственно. Отрезок PQ
— средняя линия треугольника BCD
, поэтому MK\parallel BD
, а так как OC\perp BD
, то MK\perp OC
. Кроме того, точка H
пересечения OC
и MK
— середина отрезков OC
и PQ
, а так как диаметр, перпендикулярный хорде, делит её пополам, то H
— середина хорды MK
. Значит, AH
— высота и медиана треугольника AMK
, поэтому треугольник PAQ
равнобедренный, AM=AK
.
Поскольку AO:OH=2:1
, то O
— точка пересечения его медиан. Пусть прямая MO
пересекает сторону AK
в точке F
. Тогда F
— середина AK
, а так как O
— центр описанной окружности треугольника AMK
, то содержащая точку O
прямая MF
— серединный перпендикуляр к стороне AK
. Значит, MA=MK
. Следовательно, равнобедренный треугольник AMK
— равносторонний.
б) Обозначим AM=AK=MK=x
. Тогда AH=\frac{x\sqrt{3}}{2}
. С другой стороны, так как O
— центр треугольника AMK
, то
AH=\frac{3}{2}OA=\frac{3}{2}\cdot\frac{\sqrt{2}}{2}=\frac{3\sqrt{2}}{4}.
Из равенства \frac{x\sqrt{3}}{2}=\frac{3\sqrt{2}}{4}
находим, что x=\frac{\sqrt{6}}{2}
. Следовательно,
S_{\triangle AMK}=\frac{1}{2}MK\cdot AH=\frac{1}{2}\cdot\frac{\sqrt{6}}{2}\cdot\frac{3\sqrt{2}}{4}=\frac{3\sqrt{3}}{8}.
Источник: ЕГЭ. — 2016
