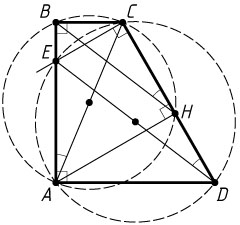
6870. В трапеции ABCD
боковая сторона AB
перпендикулярна основаниям. Из точки A
на сторону CD
опустили перпендикуляр AH
. Перпендикуляр, восставленный к той же стороне в точке C
, пересекает сторону AB
в точке E
.
а) Докажите, что BH\parallel ED
.
б) Найдите отношение BH:ED
, если \angle ADC=60^{\circ}
.
Ответ. 0,75.
Указание. Точки A
, B
, C
и H
лежат на одной окружности; точки A
, E
, C
и D
также лежат на одной окружности.
Решение. а) Из точек B
и H
отрезок AC
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AC
. Вписанные в эту окружность углы BHC
и BAC
опираются на одну и ту же дугу, поэтому \angle BHC=\angle BAC
.
Из точек A
и C
отрезок DE
виден под прямым углом, значит, эти точки лежат на окружности с диаметром DE
. Вписанные в эту окружность углы CAE
и CDE
опираются на одну и ту же дугу, поэтому \angle BAC=\angle CAE=\angle CDE
. Значит, \angle BHC=\angle CDE
.
Соответственные углы BHC
и EDC
при прямых BH
, ED
и секущей CD
равны, следовательно, эти прямые параллельны.
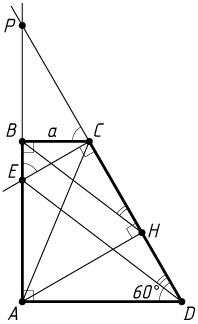
б) Пусть прямые AB
и CD
пересекаются в точке P
. Тогда
\angle PEC=\angle BCP=\angle ADC=60^{\circ}.
Обозначим BC=a
. Тогда
PB=BC\tg60^{\circ}=a\sqrt{3},~BE=BC\ctg60^{\circ}=\frac{a}{\sqrt{3}}.
Значит,
PE=PB+BE=a\sqrt{3}+\frac{a}{\sqrt{3}}=\frac{4a\sqrt{3}}{3}.
Треугольник PBH
подобен треугольнику PED
, следовательно,
\frac{BH}{ED}=\frac{PB}{PE}=\frac{a\sqrt{3}}{\frac{4a\sqrt{3}}{3}}=\frac{3}{4}=0{,}75.
Источник: ЕГЭ. — 2016

