6871. Окружности \Omega_1
и \Omega_2
с центрами O_1
и O_2
касаются внешним образом в точке A
. Общая внешняя касательная к этим окружностям касается \Omega_1
и \Omega_2
соответственно в точках B_1
и B_2
. Общая касательная к окружностям, проходящая через точку A
, пересекает отрезок B_1B_2
в точке C
. Прямая, делящая угол ACO_2
пополам, пересекает прямые O_1B_1
, O_1O_2
, O_2B_2
в точках D_1
, L
, D_2
соответственно. Найдите отношение LD_2:O_2D_2
, если известно, что CD_1=CO_1
.
Ответ. 1:1
.
Указание. Докажите, что треугольник CO_{1}L
равнобедренный.
Решение. Центр окружности, вписанной в угол, лежит на его биссектрисе, биссектрисы смежных углов перпендикулярны, поэтому \angle O_{1}CO_{2}=90^{\circ}
, а CA
— высота прямоугольного треугольника O_{1}CO_{2}
, проведённая из вершины прямого угла.
Пусть \angle ACB_{2}=4\alpha
. Тогда
\angle ACO_{2}=2\alpha,~\angle ACL=\angle O_{2}CL=\alpha,~\angle CO_{1}L=\angle CO_{1}A=\angle ACO_{2}=2\alpha,
\angle O_{1}LC=90^{\circ}-\angle ACL=90^{\circ}-\alpha,~\angle O_{1}CL=90^{\circ}-\angle O_{2}CL=90^{\circ}-\alpha.
Значит, треугольник CO_{1}L
равнобедренный, O_{1}L=O_{1}C
.
Луч O_{1}C
— биссектриса угла AO_{1}B_{1}
, поэтому
\angle CD_{1}O_{1}=\angle CO_{1}D_{1}=\angle CO_{1}A=2\alpha.
Прямые B_{2}D_{2}
и O_{1}D_{1}
перпендикулярны одной и той же прямой B_{1}B_{2}
, значит, B_{2}D_{2}\parallel O_{1}D_{1}
. Тогда
\angle LD_{2}O_{2}=\angle CD_{1}O_{2}=2\alpha,
а так как
\angle D_{2}LO_{2}=\angle CLA=90^{\circ}-\alpha,
то
\angle LO_{2}D_{2}=180^{\circ}-2\alpha-(90^{\circ}-\alpha)=90^{\circ}-\alpha=\angle DLO_{2}.
Значит, треугольник LO_{2}D_{2}
равнобедренный, и LD_{2}=O_{2}D_{2}
. Следовательно, LD_{2}:O_{2}D_{2}=1:1
.
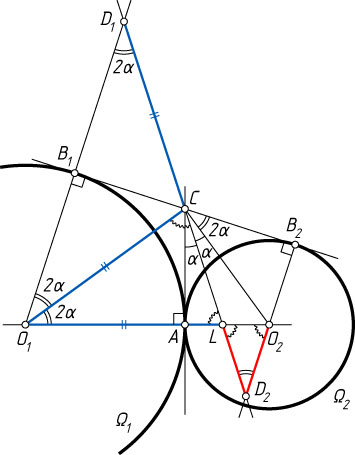
Примечание. Сумма углов треугольника D_{1}O_{1}L
равна 180^{\circ}
, т. е. 2\alpha+4\alpha+(90^{\circ}-\alpha)=180^{\circ}
, откуда \alpha=18^{\circ}
. В приведённом решении нам это не понадобилось.
Источник: Дополнительное вступительное испытание в МГУ. — 2014, июль, вариант 1, № 5
