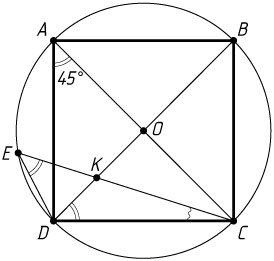
6879. Квадрат ABCD
вписан в окружность. Хорда CE
пересекает диагональ BD
в точке K
.
а) Докажите, что произведение CK\cdot CE
равно площади квадрата.
б) Найдите отношение CK:KE
, если \angle ECD=15^{\circ}
.
Ответ. 2:1
.
Указание. Треугольники CDK
и CED
подобны.
Решение. а) Вписанные углы CED
и CAD
опираются на одну и ту же дугу, поэтому
\angle CED=\angle CAD=\angle CDK=45^{\circ}.
Треугольник CDK
подобен треугольнику CED
по двум углам, поэтому \frac{CD}{CE}=\frac{CK}{CD}
. Следовательно,
CE\cdot CK=CD^{2}=S_{ABCD}.
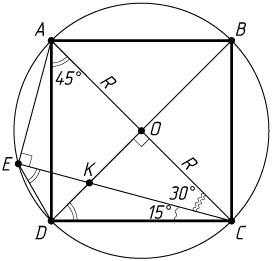
б) Пусть O
— центр окружности, а её радиус равен R
. Точка E
лежит на окружности с диаметром AC
, значит, \angle AEC=90^{\circ}
, а так как
\angle ACE=\angle ACD-\angle ECD=45^{\circ}-15^{\circ}=30^{\circ},
из прямоугольного треугольника ACE
находим, что
CE=AC\cos30^{\circ}=2R\cdot\frac{\sqrt{3}}{2}=R\sqrt{3}.
Из прямоугольного треугольника COK
находим также, что
CK=\frac{OC}{\cos30^{\circ}}=\frac{R}{\frac{\sqrt{3}}{2}}=\frac{2R}{\sqrt{3}}.
Значит,
\frac{CK}{CE}=\frac{\frac{2R}{\sqrt{3}}}{R\sqrt{3}}=\frac{2}{3}.
Следовательно, CK:KE=2:1
.
Источник: ЕГЭ. — 2016

