6882. В окружности с центром в точке O
проведена хорда PQ
, не являющаяся диаметром. Также проведён диаметр AB
, перпендикулярный PQ
. Пусть B
лежит на большей дуге PQ
, а на меньшей дуге возьмём произвольную точку M
. На луче MB
возьмём точку L
так, чтобы B
являлась центром описанной окружности треугольника PQL
. Пусть K
— точка пересечения исходной окружности с отрезком PL
. Докажите, что прямая OK
делит дугу MQ
пополам.
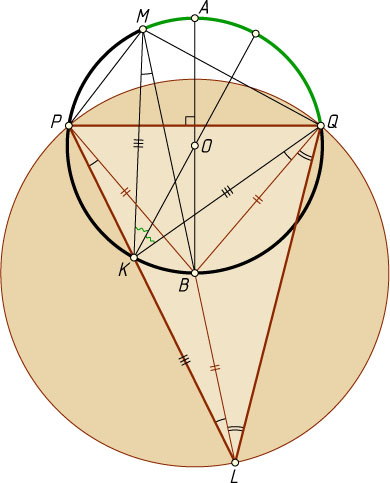
Решение. Поскольку B
— центр описанной окружности треугольника PQL
, то BQ=BP=BL
, поэтому
\angle BLP=\angle BPK=\angle BMK,
значит, треугольник MKL
равнобедренный, KL=KM
. Кроме того,
\angle BQL=\angle BLQ,~\angle BQK=\angle BPK=\angle BLK.
Значит,
\angle KQL=\angle BQK+\angle BQL=\angle BLK+\angle BLQ=\angle KLQ,
поэтому треугольник QKL
также равнобедренный, KQ=KL=KM
. Точка O
равноудалена от равных хорд KQ
и KM
, следовательно, KO
— биссектриса вписанного угла MKQ
, а значит, проходит через середину дуги MQ
.
Автор: Домбровский Г. А.
