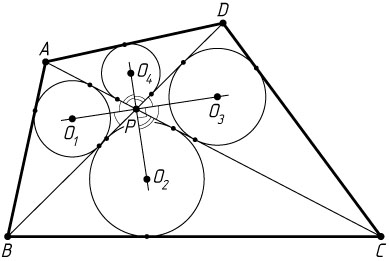
6885. Диагонали выпуклого четырёхугольника ABCD
пересекаются в точке P
. В треугольники APB
, BPC
, CPD
и APD
вписаны окружности с центрами O_{1}
, O_{2}
, O_{3}
и O_{4}
соответственно.
а) Докажите, что прямые O_{1}O_{3}
и O_{2}O_{4}
перпендикулярны.
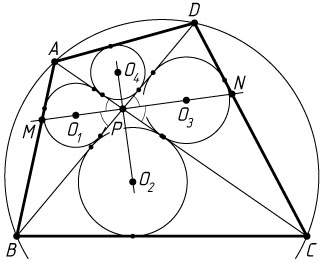
б) Пусть прямая O_{1}O_{3}
пересекает стороны AB
и CD
в точках M
и N
соответственно. Найдите отношение площадей треугольников CPN
и DPN
, если известно, что около четырёхугольника ABCD
можно описать окружность и AM:MB=1:2
.
Ответ. 2:1
.
Решение. а) Центр окружности, вписанной в треугольник, есть точка пересечения его биссектрис, а так как биссектрисы вертикальных углов лежат на одной прямой, то прямые O_{1}O_{3}
и O_{2}O_{4}
пересекаются в точке P
. Биссектрисы смежных углов перпендикулярны, поэтому \angle O_{1}PO_{2}=90^{\circ}
. Следовательно, прямые O_{1}O_{3}
и O_{2}O_{4}
перпендикулярны.
б) По свойству биссектрисы треугольника \frac{AM}{MB}=\frac{PA}{PB}
и \frac{DN}{CN}=\frac{PD}{PC}
. По теореме о произведениях отрезков пересекающихся хорд PA\cdot PC=PB\cdot PD
, поэтому \frac{PA}{PB}=\frac{PD}{PC}
. Значит,
\frac{DN}{CN}=\frac{AM}{MB}=\frac{1}{2}.
Следовательно,
\frac{S_{\triangle CPN}}{S_{\triangle DPN}}=\frac{CN}{ND}=2.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2015
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 7.43.1, с. 73

