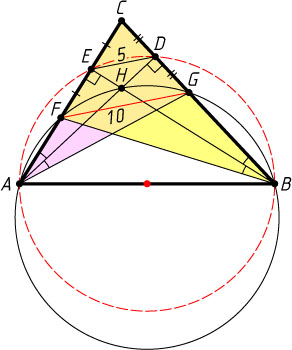
6890. Высоты AD
и BE
остроугольного треугольника ABC
пересекаются в точке H
. Окружность, описанная около треугольника ABH
, пересекает стороны AC
и BC
в точках F
и G
соответственно. Найдите FG
, если DE=5
.
Ответ. 10.
Указание. BE
— биссектриса треугольника CBF
.
Решение. Вписанные углы FAH
и FBH
опираются на одну и ту же дугу, поэтому
\angle FBE=\angle FBH=\angle FAH=\angle CAD=\angle CBE.
В треугольнике CBF
высота BE
является биссектрисой, значит, этот треугольник равнобедренный. Тогда BE
— его медиана. Значит, E
— середина CF
. Аналогично D
— середина CG
, поэтому DE
— средняя линия треугольника CFG
. Следовательно, FG=2DE=10
.
Источник: Всероссийская олимпиада школьников. — 2013-2014, XL, окружной этап, 9 класс
Источник: Избранные задачи окружных олимпиад по математике в Москве / Сост. А. Д. Блинков. — М.: МЦНМО, 2015. — № 9.5, с. 90
