6897. Точка D
на стороне BC
остроугольного треугольника ABC
такова, что AB=AD
. Окружность, описанная около треугольника ABD
, пересекает сторону AC
в точках A
и K
. Прямая DK
пересекает прямую, проходящую точку B
перпендикулярно AC
, в точке L
. Докажите, что CL=BC
.
Решение. Вписанные углы AKB
и ADB
опираются на одну и ту же дугу, поэтому
\angle AKB=\angle ADB=\angle ABD.
Четырёхугольник ABDK
вписанный, поэтому
\angle AKL=180^{\circ}-\angle AKD=\angle ABD.
Значит, \angle AKB=\angle AKL
.
Пусть P
— точка пересечения прямых AC
и BL
. Прямоугольные треугольники BPK
и LPK
равны по катету и прилежащему острому углу, поэтому прямая PK
(т. е. AC
) — серединный перпендикуляр к отрезку BL
. Следовательно, CL=BC
.
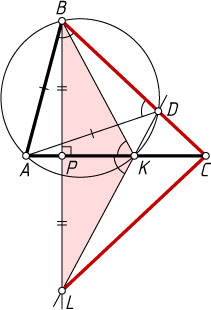
Автор: Богданов И. И.
Источник: Всероссийская олимпиада школьников. — 2008-2009, XXXV, региональный этап, 11 класс
Источник: Журнал «Квант». — 2009, № 2, с. 54
