6899. Биссектриса угла C
треугольника ABC
пересекает его описанную окружность вторично в точке R
и пересекает серединные перпендикуляры к сторонам AC
и BC
в точках P
и Q
соответственно. Точки K
и L
— середины отрезков AC
и BC
соответственно. Докажите, что площади треугольников RPK
и RQL
равны.
Решение. Серединные перпендикуляры к сторонам AC
и BC
пересекаются в центре O
описанной окружности треугольника ABC
. Прямоугольные треугольники CKP
и CLQ
подобны, поэтому \frac{PK}{QL}=\frac{CP}{CQ}
и
\angle OQP=\angle CQL=\angle CPK=\angle QPO.
Значит, PK\cdot CQ=QL\cdot CP
, а треугольник OPQ
равнобедренный с основанием PQ
. Его медиана OM
является высотой, а так как M
— середина хорды CR
(см. задачу 1676), то CP=QR
и PR=CQ
. Тогда
\frac{S_{\triangle RPK}}{S_{\triangle RQL}}=\frac{\frac{1}{2}PK\cdot PR\sin\angle KPR}{\frac{1}{2}QL\cdot QR\sin\angle LQR}=\frac{PK\cdot PR}{QL\cdot QR}=\frac{PK\cdot CQ}{QL\cdot CP}=1.
Следовательно, S_{\triangle RPK}=S_{\triangle RQL}
.
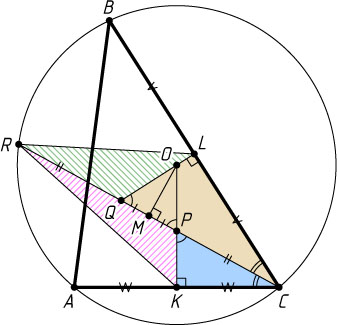
Источник: Международная математическая олимпиада. — 2007, XLVIII
