6921. В равнобедренном треугольнике ABC
(AB=AC
) проведена биссектриса BL
. Её длина равна разности BC-AL
. Найдите углы треугольника ABC
.
Ответ. 100^{\circ}
, 40^{\circ}
, 40^{\circ}
.
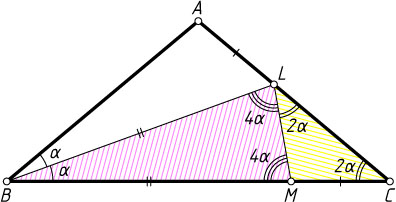
Решение. На основании BC
треугольника ABC
отложим отрезок CM=AL
. Тогда
BM=BC-CM=BC-AL=BL,
т. е. треугольник BLM
равнобедренный. Обозначим \angle ABL=\angle CBL=\alpha
. Тогда \angle LCM=\angle ABC=2\alpha
.
По свойству биссектрисы треугольника
\frac{AB}{BC}=\frac{AL}{LC}=\frac{CM}{LC},
значит, треугольник MLC
подобен треугольнику ABC
по по двум сторонам и углу между ними. Тогда \angle CLM=\angle LMC=2\alpha
. По теореме о внешнем угле треугольника \angle BML=4\alpha
. Из равнобедренного треугольника BLM
получаем, что 4\alpha+4\alpha+\alpha=180^{\circ}
, откуда \alpha=20^{\circ}
. Следовательно,
\angle ABC=\angle ACB=2\alpha=40^{\circ},~\angle BAC=100^{\circ}.
Источник: Математическая олимпиада МГУ «Ломоносов». — 2013-2014, отборочный этап, 9 класс
