6925. Точки B_{1}
и C_{1}
лежат на сторонах соответственно AC
и AB
треугольника ABC
, причём \angle AB_{1}C_{1}=\angle ABC
(в этом случае говорят, что прямые B_{1}C_{1}
и BC
антипараллельны). Докажите, что центр описанной окружности треугольника AC_{1}B_{1}
лежит на высоте AH
треугольника ABC
.
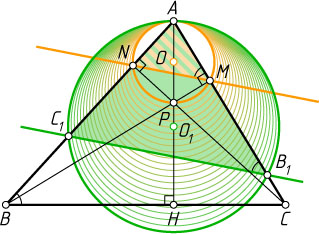
Решение. Пусть BM
и CN
— высоты треугольника ABC
, P
— точка пересечения высот. Тогда (см. задачу 141)
\angle AMN=\angle ABC=\angle AB_{1}C_{1},
значит, B_{1}C_{1}\parallel MN
. При гомотетии с центром A
, переводящей точку B_{1}
в M
, треугольник AB_{1}C_{1}
переходит в треугольник AMN
, описанная окружность треугольника AB_{1}C_{1}
— в описанную окружность треугольника AMN
, а центр O_{1}
первой окружности — в центр O
второй. Значит, точки A
, O_{1}
и O
лежат на одной прямой. Поскольку из точек M
и N
отрезок AP
виден под прямым углом, центр O
описанной окружности треугольника AMN
— середина её диаметра AP
. Следовательно, точка O_{1}
лежит на прямой AP
, а значит, на высоте AH
треугольника ABC
. Что и требовалось доказать.