6931. Боковые стороны AB
и CD
трапеции ABCD
равны соответственно 24 и 25, а основание BC
равно 9. Биссектриса угла ADC
проходит через середину стороны AB
. Найдите площадь трапеции.
Ответ. 300.
Решение. Пусть M
— середина стороны AB
, а прямые DM
и BC
пересекаются в точке P
. Тогда
\angle CPD=\angle ADP=\angle CDP,
значит, треугольник CPD
равнобедренный,
CP=CD=25,~BP=CP-BC=25-9=16,
а так как треугольники AMD
и BMP
равны (по стороне и двум прилежащим к ней углам), то AD=BP=16
.
Пусть прямая, проходящая через точку C
параллельно AB
пересекает основание AD
в точке K
. Тогда
CK=AB=24,~AK=BC=9,~DK=AD-AK=16-9=7.
Треугольник CKD
прямоугольный с прямым углом при вершине K
, так как
CK^{2}+DK^{2}=24^{2}+7^{2}=25^{2}=CD^{2}.
Значит, \angle BAD=\angle CKD=90^{\circ}
, т. е. трапеция ABCD
прямоугольная, а её высота равна 24. Следовательно,
S_{ABCD}=\frac{1}{2}(AD+BC)\cdot AB=\frac{1}{2}(16+9)\cdot24=25\cdot12=300.
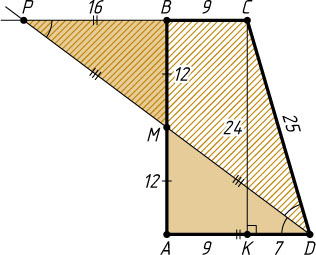
Источник: Диагностические и тренировочные задачи ОГЭ (ГИА). — 2016, задача 26
