6955. Точка O
— центр описанной окружности остроугольного треугольника ABC
. Прямая, перпендикулярная стороне AC
, пересекает отрезок BC
и прямую AB
в точках Q
и P
соответственно. Докажите, что точки B
, O
и середины отрезков AP
и CQ
лежат на одной окружности.
Решение. Пусть M
, N
, R
, S
— середины отрезков AB
, BC
, AP
и CQ
соответственно. Заметим, что OM
и ON
— серединные перпендикуляры к сторонам AB
и BC
треугольника ABC
, поэтому
\angle OMB=\angle ONB=90^{\circ},~\angle OMN=90^{\circ}-\angle NMB=90^{\circ}-\angle BAC=\angle BPQ.
Аналогично \angle ONM=\angle BQP
. Следовательно, треугольники OMN
и BPQ
подобны. Значит, \frac{OM}{ON}=\frac{BP}{BQ}
. Тогда
MR=AR-AM=\frac{1}{2}AP-\frac{1}{2}AB=\frac{1}{2}BP.
Аналогично NS=\frac{1}{2}BQ
. Таким образом,
\frac{MR}{NS}=\frac{\frac{1}{2}BP}{\frac{1}{2}BQ}=\frac{BP}{BQ}=\frac{OM}{ON},
и прямоугольные треугольники OMR
и ONS
подобны. Из последнего подобия получаем, что \angle ORM=\angle OSN
, значит,
\angle ORB+\angle OSB=180^{\circ},
и четырёхугольник ORBS
вписанный. Что и требовалось доказать.
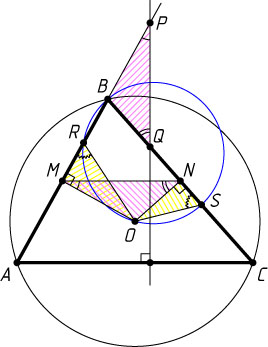
Автор: Бакаев Е. В.
Источник: Московская математическая олимпиада. — 2016, LXXIX, 9 класс
