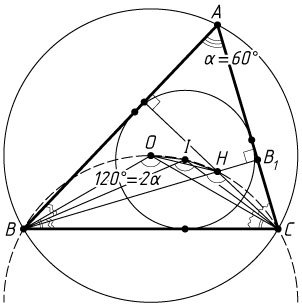
6960. Точка O
— центр окружности, описанной около остроугольного треугольника ABC
, I
— центр вписанной в него окружности, H
— точка пересечения высот. Известно, что \angle BAC=\angle OBC+\angle OCB
.
а) Докажите, что точка I
лежит на окружности, описанной около треугольника BOC
.
б) Найдите угол OIH
, если \angle ABC=55^{\circ}
.
Ответ. 175^{\circ}
.
Решение. а) Обозначим \angle A=\alpha
. Тогда
\angle BOC=2\alpha,~\angle OBC+\angle OCB=\alpha,
а так как сумма углов треугольника BOC
равна 180^{\circ}
, то 2\alpha+\alpha=180^{\circ}
, откуда \alpha=60^{\circ}
, \angle BOC=120^{\circ}
.
Точка I
— центр вписанной окружности треугольника ABC
, поэтому BI
и CI
— биссектрисы его углов. Значит,
\angle BIC=90^{\circ}+\frac{1}{2}\angle A=90^{\circ}+30^{\circ}=120^{\circ},
а так как H
— точка пересечения высот треугольника ABC
, то
\angle BHC=180^{\circ}-\angle A=180^{\circ}-60^{\circ}=120^{\circ}.
Таким образом, из точек O
, I
и H
сторона BC
видна под одним и тем же углом 120^{\circ}
, следовательно, точки B
, C
, O
, I
и H
лежат на одной окружности — окружности, описанной около треугольника BOC
.
б) Пусть BB_{1}
— высота треугольника ABC
. Тогда
\angle ABH=\angle ABB_{1}=90^{\circ}-\angle BAB_{1}=90^{\circ}-60^{\circ}=30^{\circ}.
Углы при основании BC
равнобедренного треугольника BOC
равны по 30^{\circ}
, поэтому
\angle ABO=\angle ABC-\angle ABB_{1}=55^{\circ}-30^{\circ}=25^{\circ}.
Следовательно,
\angle OBH=\angle ABH-\angle ABO=30^{\circ}-25^{\circ}=5^{\circ},
а так как четырёхугольник BOIH
вписанный, то
\angle OIH=180^{\circ}-\angle OBH=180^{\circ}-5^{\circ}=175^{\circ}.
Источник: ЕГЭ. — 2016
