6992. На плоскости даны точки A
, B
и C
. Найдите геометрическое место точек M
плоскости таких, что прямая, проходящая через M
и перпендикулярная CM
, пересекает отрезок AB
.
Ответ. Точки, принадлежащие ровно одному из кругов, построенных на отрезках AC
и BC
как на диаметрах.
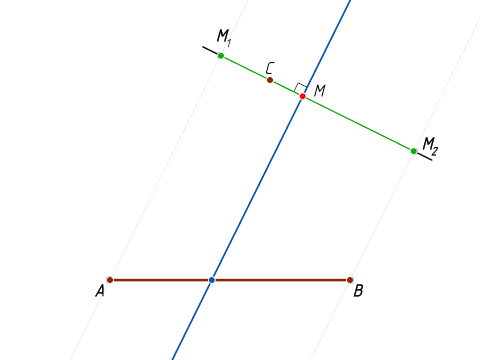
Решение. Построим на отрезках AC
и BC
как на диаметрах окружности. Проведём через точку C
прямую, пересекающую эти окружности в точках M_{1}
и M_{2}
(отличных от C
). Ясно что среди точек этой прямой искомому ГМТ все точки отрезка M_{1}M_{2}
, и только они. Таким образом, искомое ГМТ состоит из точек, принадлежащих ровно одному из кругов, построенных на отрезках AC
и BC
как на диаметрах.
 <
<

Источник: Соросовская олимпиада. — 1994, I, III тур, 1-й раунд, 9 класс
 <
<
