7005. Сторона основания правильной треугольной пирамиды равна a
. Боковое ребро образует с плоскостью основания угол 60^{\circ}
. Найдите расстояние между противоположными рёбрами пирамиды.
Ответ. \frac{3a}{4}
.
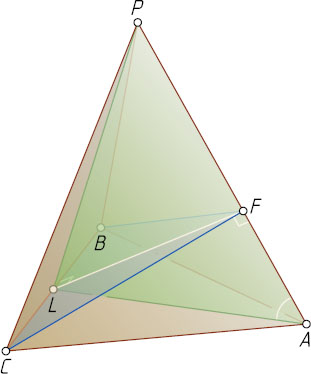
Решение. Пусть PABC
— правильная треугольная пирамида с вершиной P
, M
— центр основания ABC
, F
— основание перпендикуляра, опущенного из середины L
ребра BC
на прямую AP
.
Прямая AL
— ортогональная проекция наклонной AP
на плоскость основания пирамиды. По теореме о трёх перпендикулярах AP\perp BC
, поэтому прямая AP
перпендикулярна двум пересекающимся прямым AP
и BC
плоскости BFC
. Значит, прямая AP
перпендикулярна плоскости BFC
, поэтому FL
— общий перпендикуляр скрещивающихся прямых AP
и BC
. Из прямоугольного треугольника AFL
находим, что
FL=AL\sin\angle FAL=AL\sin\angle PAM=\frac{a\sqrt{3}}{2}\cdot\sin60^{\circ}=\frac{3a}{4}.