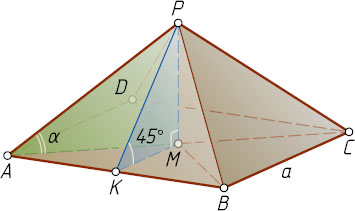
7013. Боковая грань правильной четырёхугольной пирамиды образует с плоскостью основания угол 45^{\circ}
. Найдите угол бокового ребра с плоскостью основания.
Ответ. \arctg\frac{\sqrt{2}}{2}
.
Решение. Пусть ABCDP
— данная правильная четырёхугольная пирамида с вершиной P
, AB=BC=CD=AD=a
, M
— центр квадрата ABCD
, K
— середина отрезка AB
.
Поскольку PK\perp AB
и MK\perp AB
, угол PKM
— линейный угол двугранного угла между плоскостью боковой грани ABP
и плоскостью основания пирамиды. По условию \angle PKM=45^{\circ}
.
Поскольку пирамида правильная, её высота проходит через центр основания, значит, PM
— высота пирамиды. Из равнобедренного прямоугольного треугольника PKM
находим, что PM=MK=\frac{a}{2}
.
Пусть \alpha
— угол бокового ребра с плоскостью основания пирамиды. Из прямоугольного треугольника AMP
находим, что
\tg\alpha=\tg\angle MAP=\frac{PM}{AM}=\frac{\frac{a}{2}}{\frac{a\sqrt{2}}{2}}=\frac{\sqrt{2}}{2}.