7014. Боковая грань правильной четырёхугольной пирамиды образует с плоскостью основания угол 45^{\circ}
. Найдите угол между противоположными боковыми гранями.
Ответ. 90^{\circ}
.
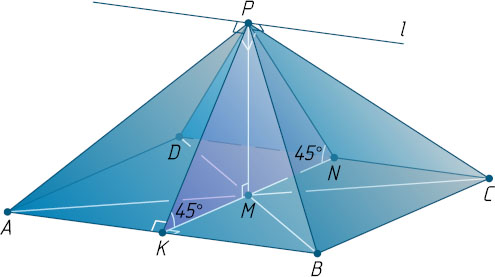
Решение. Пусть ABCDP
— данная правильная четырёхугольная пирамида с вершиной P
, AB=BC=CD=AD=a
, M
— центр квадрата ABCD
, K
и N
— середины отрезков AB
и CD
соответственно.
Поскольку PK\perp AB
и MK\perp AB
, угол PKM
— линейный угол двугранного угла между плоскостью боковой грани ABP
и плоскостью основания пирамиды. По условию \angle PNM=\angle PKM=45^{\circ}
.
Плоскости боковых граней ABP
и CDP
проходят через параллельные прямые AB
и CD
и имеют общую точку P
, поэтому они пересекаются по прямой l
, проходящей через точку P
параллельно прямым AB
и CD
, причём PK\perp l
и PN\perp l
. Значит, линейный угол двугранного угла между противоположными боковыми гранями PAB
и PCD
— это угол KPN
. Из равнобедренного треугольника KPN
находим, что
\angle KPN=180^{\circ}-\angle PKN-\angle PNK=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}.