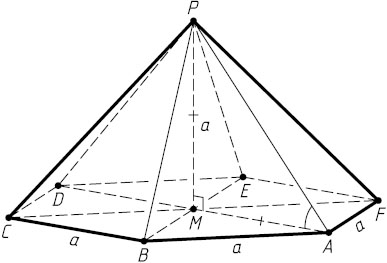
7021. Высота правильной шестиугольной пирамиды равна стороне основания. Найдите угол бокового ребра с плоскостью основания.
Ответ. 45^{\circ}
.
Решение. Пусть ABCDEFP
— данная правильная шестиугольная пирамида с вершиной P
; M
— центр правильного шестиугольника ABCDEF
. Обозначим AB=BC=CD=DE=EF=AF=a
.
Поскольку пирамида правильная, PM
— её высота. Значит, угол бокового ребра с плоскостью основания — это угол PAM
. В прямоугольном треугольнике APM
известно, что PM=AM=a
, поэтому \angle PAM=45^{\circ}
.