7040. Найдите высоту правильного тетраэдра с ребром a
.
Ответ. a\sqrt{\frac{2}{3}}
.
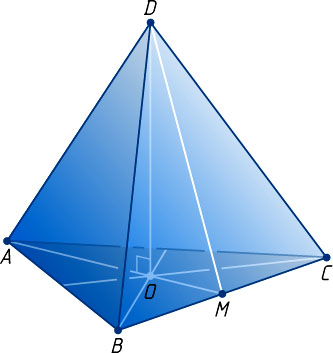
Решение. Пусть ABCD
— правильный тетраэдр, DO
— его высота, M
— середина BC
. Так как AM
— высота равностороннего треугольника ABC
, а O
— центр этого треугольника, то
AM=\frac{a\sqrt{3}}{2},~OA=\frac{2}{3}AM=\frac{a\sqrt{3}}{3}.
Из прямоугольного треугольника OAD
находим, что
DO=\sqrt{DA^{2}-OA^{2}}=\sqrt{a^{2}-\left(\frac{a\sqrt{3}}{3}\right)^{2}}=a\sqrt{1-\frac{1}{3}}=a\sqrt{\frac{2}{3}}.
Источник: Шарыгин И. Ф. Геометрия: Учебник для 10—11 кл. общеобразовательных учебных заведений. — М.: Дрофа, 1999. — № 4, с. 66
