7043. Найдите площадь сечения, проведённого через высоту и одно из рёбер правильного тетраэдра, если ребро тетраэдра равно a
.
Ответ. \frac{a^{2}\sqrt{2}}{4}
.
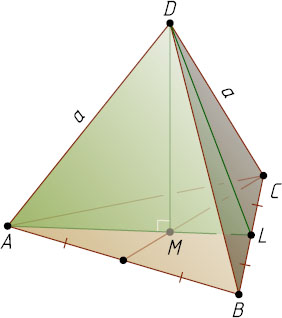
Решение. Пусть ABCD
— правильный тетраэдр с ребром a
, M
— центр грани ABC
. Поскольку DM
— высота тетраэдра, треугольник AMD
прямоугольный. По теореме Пифагора находим, что
DM=\sqrt{AD^{2}-AM^{2}}=\sqrt{a^{2}-\left(\frac{a\sqrt{3}}{3}\right)^{2}}=a\sqrt{1-\frac{1}{3}}=a\sqrt{\frac{2}{3}}.
Плоскость, проведённая через ребро AD
и высоту DM
, пересекает ребро BC
в его середине L
. Искомое сечение — треугольник ADL
с высотой DM
и основанием AL
. Поскольку DM=a\sqrt{\frac{2}{3}}
, а AL=\frac{a\sqrt{3}}{2}
, то
S_{\triangle ADL}=\frac{1}{2}AL\cdot DM=\frac{1}{2}\cdot\frac{a\sqrt{3}}{2}\cdot a\sqrt{\frac{2}{3}}=\frac{a^{2}\sqrt{2}}{4}.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 7.1, с. 62
