7044. В правильном тетраэдре найдите угол между ребром и плоскостью грани, не содержащей это ребро.
Ответ. \arccos\frac{1}{\sqrt{3}}
.
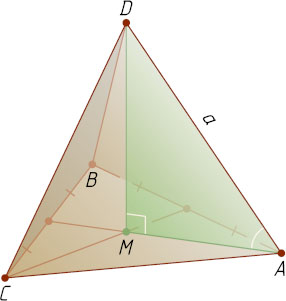
Решение. Пусть ABCD
— правильный тетраэдр с ребром a
, M
— центр грани ABC
. Поскольку DM
— высота тетраэдра, искомый угол между ребром AD
и плоскостью грани ABC
— это угол DAM
. Обозначим его \alpha
. В прямоугольном треугольнике DAM
известно, что AD=a
, AM=\frac{a\sqrt{3}}{3}
. Следовательно,
\cos\alpha=\cos\angle DAM=\frac{AM}{AD}=\frac{\frac{a\sqrt{3}}{3}}{a}=\frac{\sqrt{3}}{3}=\frac{1}{\sqrt{3}}.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2(а), с. 44
