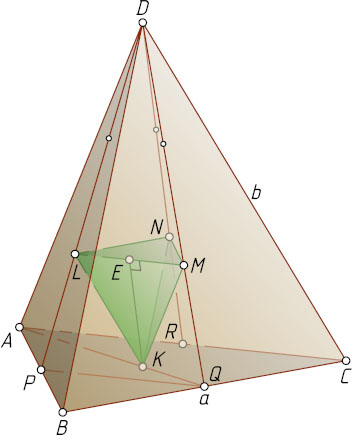
7093. Вершины пирамиды KLMN
расположены в точках пересечения медиан граней некоторой правильной треугольной пирамиды со стороной основания a
и боковым ребром b
. Найдите полную поверхность пирамиды KLMN
.
Ответ. \frac{a(3\sqrt{4b^{2}-a^{2}}+a\sqrt{3})}{36}
.
Указание. Докажите, что KLMN
— правильная треугольная пирамида со стороной основания \frac{a}{3}
и боковым ребром \frac{b}{3}
.
Решение. Пусть K
— центр основания ABC
правильной треугольной пирамиды ABCD
; L
, M
и N
— точки пересечения медиан боковых граней ADB
, BDC
и ADC
соответственно; P
, Q
и R
— середины рёбер AB
, BC
и AC
.
В треугольнике PDQ
точки L
и M
делят стороны DP
и DQ
в одном и том же отношении
\frac{DL}{LP}=\frac{DM}{MQ}=2.
Поэтому
LM=\frac{2}{3}PQ=\frac{2}{3}\cdot\frac{1}{2}AC=\frac{a}{3}.
Аналогично MN=LN=\frac{a}{3}
.
В треугольнике AQD
точки K
и M
делят стороны AQ
и DQ
в одном и том же отношении
\frac{QK}{AQ}=\frac{QM}{DQ}=\frac{1}{3}.
Поэтому KM=\frac{1}{3}AD=\frac{b}{3}
. Аналогично KL=KN=\frac{b}{3}
.
Таким образом, основание LMN
треугольной пирамиды KLMN
— равносторонний треугольник, а боковые рёбра KL
, KM
и KN
равны между собой. Следовательно, это правильная пирамида со стороной основания \frac{a}{3}
и боковым ребром \frac{b}{3}
. Площадь её основания
S_{\triangle LMN}=LM^{2}\cdot\frac{\sqrt{3}}{4}=\frac{a^{2}\sqrt{3}}{36}.
Пусть KE
— высота равнобедренного треугольника KLM
(апофема пирамиды KLMN
). Тогда
KE=\sqrt{KM^{2}-EM^{2}}=\sqrt{\left(\frac{b}{3}\right)^{2}-\left(\frac{a}{6}\right)^{2}}=\frac{\sqrt{4b^{2}-a^{2}}}{6}.
Значит,
S_{\triangle KLM}=\frac{1}{2}LM\cdot KE=\frac{a\sqrt{4b^{2}-a^{2}}}{36}.
Следовательно, полная поверхность пирамиды KLMN
равна
S_{\triangle LMN}+3S_{\triangle KLM}=\frac{a\sqrt{4b^{2}-a^{2}}}{12}+\frac{a^{2}\sqrt{3}}{36}=\frac{a(3\sqrt{4b^{2}-a^{2}}+a\sqrt{3})}{36}.