7103. Докажите, что отрезки, соединяющие середины противоположных рёбер тетраэдра (бимедианы тетраэдра) пересекаются в одной точке.
Указание. Докажите, что любые два таких отрезка пересекаются и точкой пересечения делятся пополам.
Решение. Первый способ. Докажем, что любые два таких отрезка пересекаются и точкой пересечения делятся пополам.
Пусть M
, N
, K
и L
— середины рёбер соответственно AB
, CD
, BC
и AD
тетраэдра ABCD
. Поскольку LN
и MK
— средние линии треугольников ADC
и ABC
с общим основанием AC
, LN\parallel MK
и LN=MK
. Поэтому прямые LN
и MK
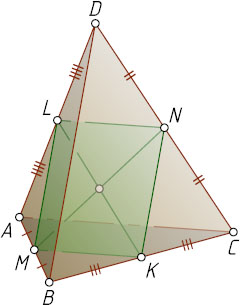
лежат в одной плоскости, а четырёхугольник MLNK
— параллелограмм. Следовательно, отрезки MN
и KL
пересекаются и делятся точкой пересечения пополам.
Отрезок, соединяющий середины противоположных рёбер AC
и BD
, должен разделить каждый из отрезков MN
и KL
пополам, т. е. пройти через их точку пересечения.
Второй способ. Поместим в вершины тетраэдра ABCD
одинаковые массы m
. Тогда центр масс точек A
и B
— середина P
ребра AB
, а центр масс точек C
и D
— середина Q
ребра CD
Поместим в точки P
и Q
массы 2m
. Тогда центр масс точек A
, B
, C
и D
— середина O
отрезка PQ
. Из единственности центра масс следует, что остальные такие отрезки также проходят через точку O
и делятся ею пополам.
Третий способ. Достроим тетраэдр ABCD
до параллелепипеда ALBKMCND
, проведя через противоположные рёбра пары параллельных плоскостей (ALBK
и MCDN
— противоположные грани, AM\parallel LC\parallel BN\parallel KD
). Пусть P
и Q
— середины рёбер AB
и CD
тетраэдра. Тогда P
и Q
— центры параллелограммов ALBK
и MCDN
. Отрезок PQ
проходит через центр O
параллелепипеда и делится им пополам. Аналогично для двух остальных таких отрезков. Следовательно, отрезки, соединяющие середины противоположных рёбер тетраэдра, проходят через точку O
и делятся ею пополам.
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 390(б), с. 59
