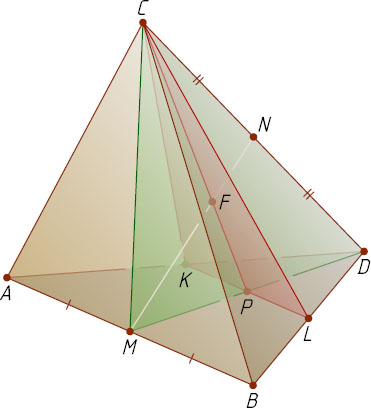
7128. Через вершину C
тетраэдра ABCD
и середины рёбер AD
и BD
проведена плоскость. В каком отношении эта плоскость делит отрезок MN
, где M
и N
— середины рёбер AB
и CD
соответственно?
Ответ. 1:2
, считая от точки N
.
Указание. Указанная плоскость пересекает отрезок MN
в точке пересечения медиан треугольника DMC
.
Решение. Пусть K
и L
— середины рёбер AD
и BD
, а P
— точка пересечения DM
и KL
. Поскольку KL
— средняя линия треугольника ABD
, а MD
— медиана, точка P
— середина DM
.
Рассмотрим сечение пирамиды ABCD
плоскостью MDC
. Отрезки MN
и CP
— медианы треугольника MDC
. Пусть они пересекаются в точке F
. Тогда NF:FM=1:2
. Осталось заметить, что в точке F
плоскость CKL
пересекает отрезок MN
.