7140. В правильную четырёхугольную пирамиду впишите прямоугольный параллелепипед наибольшего объёма так, чтобы одна грань параллелепипеда лежала в плоскости основания пирамиды, а вершины противоположной грани принадлежали боковым рёбрам.
Решение. Пусть V
— объём правильной четырёхугольной пирамиды со стороной основания ABCD
, равной a
, и высотой SH
, равной h
; V_{1}
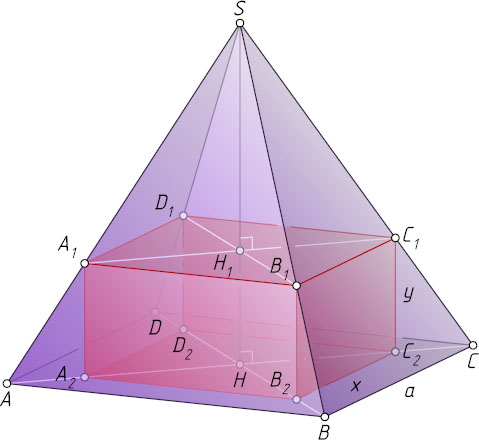
— объём прямоугольного параллелепипеда A_{1}B_{1}C_{1}D_{1}\allowbreak A_{2}B_{2}C_{2}D_{2}
, грань A_{2}B_{2}C_{2}D_{2}
которого лежит в плоскости ABCD
, а вершины A_{1}
, B_{1}
, C_{1}
, D_{1}
— на боковых рёбрах соответственно SA
, SB
, SC
, SD
пирамиды.
Пусть H_{1}
— точка пересечения высоты SH
пирамиды с плоскостью грани A_{1}B_{1}C_{1}D_{1}
параллелепипеда. Обозначим \frac{SH_{1}}{SH}=k
(0\lt k\lt1
), x
— сторона квадрата A_{2}B_{2}C_{2}D_{2}
, y
— боковое ребро параллелепипеда. Тогда
y=H_{1}H=(1-k)SH=(1-k)h,~x=ka,
V_{1}=x^{2}y=ka\cdot ka\cdot(1-k)h=a^{2}h\cdot k^{2}(1-k)=
=3V\cdot k^{2}(1-k)=12V\cdot\frac{k}{2}\cdot\frac{k}{2}\cdot(1-k)\leqslant
\leqslant12V\cdot\left(\frac{\frac{k}{2}+\frac{k}{2}+1-k}{3}\right)^{3}=12V\cdot\frac{1}{27}=\frac{4}{9}V,
причём равенство достигается в случае, когда \frac{k}{2}=1-k
, т. е. при k=\frac{2}{3}
.
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 152, с. 27
