7204. Через середину ребра правильного тетраэдра проведена плоскость, перпендикулярная соседнему ребру. Найдите площадь полученного сечения, если ребро тетраэдра равно a
.
Ответ. \frac{a^{2}\sqrt{2}}{16}
.
Указание. Пусть K
— середина ребра AD
правильного тетраэдра ABCD
. Плоскость, проходящая через точки A
, B
и середину ребра CD
, перпендикулярна ребру CD
, а значит, параллельна плоскости указанного сечения.
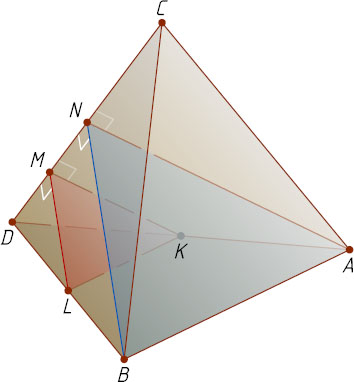
Решение. Пусть K
— середина ребра AD
правильного тетраэдра ABCD
. Если плоскость, проходящая через точку K
перпендикулярно прямой CD
, пересекает рёбра CD
и BD
в точках M
и L
, то KM\perp CD
и LM\perp CD
, поскольку прямые KM
и LM
лежат в плоскости, перпендикулярной прямой CD
.
Пусть N
— середина отрезка DC
. Тогда AN
и BN
— высоты равносторонних треугольников ACD
и BCD
. Поэтому KM\parallel AN
и LM\parallel BN
. Следовательно, KM
и LM
— средние линии треугольников AND
и BND
.
Треугольник KML
подобен треугольнику ANB
с коэффициентом \frac{1}{2}
. Следовательно, S_{\triangle KML}=\frac{1}{4}S_{\triangle ANB}
.
В равнобедренном треугольнике ANB
известны стороны
AB=a,~BN=AN=\sqrt{AC^{2}-CN^{2}}=\sqrt{a^{2}-\frac{a^{2}}{4}}=\frac{a\sqrt{3}}{2}.
Поэтому
S_{\triangle ANB}=\frac{1}{2}AB\sqrt{AN^{2}-\frac{AB^{2}}{4}}=\frac{1}{2}a\sqrt{\frac{3a^{2}}{4}-\frac{a^{2}}{4}}=\frac{a^{2}\sqrt{2}}{4}.
Следовательно, S_{\triangle KML}=\frac{a^{2}\sqrt{2}}{16}
.