7206. Через вершину D
правильного тетраэдра ABCD
с ребром a
и середины рёбер AB
и AC
проведена плоскость. Найдите площадь полученного сечения.
Ответ. \frac{a^{2}\sqrt{11}}{16}
.
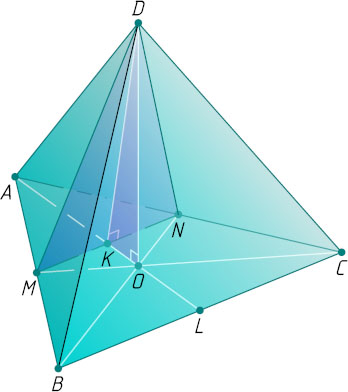
Решение. Пусть M
и N
— середины рёбер AB
и AC
соответственно. Полученное сечение — равнобедренный треугольник DMN
(равенство DM=DN
следует из равенства треугольников ADM
и ADN
).
Пусть O
— центр правильного треугольника ABC
(тогда DO
— высота тетраэдра ABCD
), K
— точка пересечения отрезка MN
с медианой AL
треугольника ABC
. Тогда K
— середина отрезков MN
и AL
, DK
— высота треугольника DMN
, а так как
AO=\frac{2}{3}AL=\frac{2}{3}\cdot\frac{1}{2}a\sqrt{3}=\frac{1}{3}a\sqrt{3},
OK=AO-AK=\frac{1}{3}a\sqrt{3}-\frac{1}{4}a\sqrt{3}=\frac{a\sqrt{3}}{12},
DO=\sqrt{AD^{2}-AO^{2}}=\sqrt{a^{2}-\frac{a^{2}}{3}}=a\sqrt{\frac{2}{3}},
то из прямоугольного треугольника DOK
находим, что
DK=\sqrt{DO^{2}+OK^{2}}=\sqrt{\frac{2a^{2}}{3}+\frac{a^{2}}{48}}=\frac{a\sqrt{11}}{4}.
Следовательно,
S_{\triangle DMN}=\frac{1}{2}MN\cdot KD=\frac{1}{2}a\cdot\frac{a\sqrt{11}}{8}=\frac{a^{2}\sqrt{11}}{16}.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2(б), с. 61
