7221. Через диагональ B_{1}D_{1}
грани A_{1}B_{1}C_{1}D_{1}
и середину ребра DC
правильной четырёхугольной призмы ABCDA_{1}B_{1}C_{1}D_{1}
проведена плоскость. Найдите площадь сечения призмы этой плоскостью, если AB=a
, CC_{1}=2a
.
Ответ. \frac{3a^{2}\sqrt{33}}{8}
.
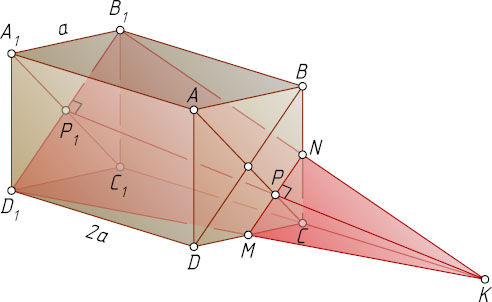
Решение. Пусть M
— середина ребра CD
. Секущая плоскость пересекает плоскость грани CC_{1}D_{1}D
по прямой D_{1}M
. Найдём точку K
пересечения прямой D_{1}M
с плоскостью грани BCC_{1}B_{1}
, продолжив отрезки D_{1}M
и C_{1}C
за точки M
и C
соответственно. Поскольку точки K
и B_{1}
лежат в секущей плоскости, прямая B_{1}K
также лежит в этой плоскости. Значит, секущая плоскость пересекает плоскость грани BCC_{1}B_{1}
по прямой KB_{1}
.
Пусть N
— точка пересечения прямой KB_{1}
с ребром BC
. Поскольку MN\parallel B_{1}D_{1}
(по теореме о пересечении двух параллельных плоскостей третьей), MN
— средняя линия треугольника CBD
. Поэтому MN\parallel BD
и MN=\frac{1}{2}BD
. Следовательно, четырёхугольник B_{1}D_{1}MN
— равнобедренная трапеция (B_{1}N=D_{1}M
из равенства прямоугольных треугольников B_{1}BN
и D_{1}DM
) с основаниями B_{1}D_{1}
и MN
(B_{1}D_{1}=a\sqrt{2}
, MN=\frac{a\sqrt{2}}{2}
), а MN
— средняя линия равнобедренного треугольника B_{1}KD_{1}
.
Пусть P_{1}
— точка пересечения диагоналей квадрата A_{1}B_{1}C_{1}D_{1}
. Тогда KP_{1}
— высота равнобедренного треугольника B_{1}KD_{1}
. Из прямоугольного треугольника KC_{1}P_{1}
находим, что
KP_{1}=\sqrt{C_{1}K^{2}+C_{1}P^{2}}=\sqrt{16a^{2}+\frac{a^{2}}{2}}=\frac{a\sqrt{33}}{\sqrt{2}}=\frac{a\sqrt{66}}{2}.
Если P
— точка пересечения отрезков MN
и AC
, то PP_{1}
— высота равнобедренной трапеции B_{1}D_{1}MN
и
PP_{1}=\frac{1}{2}KP_{1}=\frac{1}{4}a\sqrt{66}.
Следовательно,
S_{B_{1}D_{1}MN}=\frac{1}{2}(B_{1}D_{1}+MN)\cdot PP_{1}=\left(a\sqrt{2}+\frac{a\sqrt{2}}{2}\right)\cdot\frac{a\sqrt{66}}{8}=\frac{3a^{2}\sqrt{33}}{8}.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 7.7, с. 63
