7343. В правильной треугольной призме ABCA_{1}B_{1}C_{1}
, все рёбра которой равны 1, найдите косинус угла между прямыми AD_{1}
и CE_{1}
, где D_{1}
и E_{1}
— соответственно середины рёбер A_{1}C_{1}
и B_{1}C_{1}
.
Ответ. 0{,}7
Решение. Первый способ. Отрезок D_{1}E_{1}
— средняя линия треугольника A_{1}B_{1}C_{1}
, поэтому D_{1}E_{1}\parallel A_{1}B_{1}
и D_{1}E_{1}=\frac{1}{2}A_{1}B_{1}
.
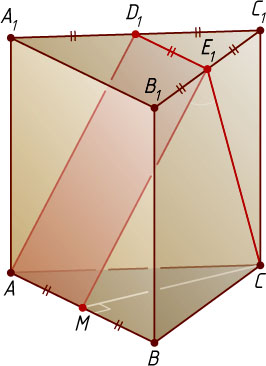
Пусть M
— середина ребра AB
. Тогда
AM=\frac{1}{2}AB=\frac{1}{2}A_{1}B_{1}=D_{1}E_{1},~AM\parallel A_{1}B_{1}\parallel D_{1}E_{1},
значит, четырёхугольник AME_{1}D_{1}
— параллелограмм. Следовательно, ME_{1}\parallel AD_{1}
, поэтому угол \alpha
между скрещивающимися прямыми AD_{1}
и CE_{1}
равен углу между пересекающимися прямыми ME_{1}
и CE_{1}
.
Из прямоугольного треугольника CC_{1}E_{1}
находим, что
CE_{1}=\sqrt{CC_{1}^{2}+C_{1}E_{1}^{2}}=\sqrt{1+\frac{1}{4}}=\frac{\sqrt{5}}{2}.
Аналогично AD_{1}=\frac{\sqrt{5}}{2}
. Отрезок CM
— медиана, а значит, высота равностороннего треугольника ABC
со стороной 1, поэтому CM=\frac{\sqrt{3}}{2}
.
В треугольнике CE_{1}M
известно, что CE_{1}=\frac{\sqrt{5}}{2}
, ME_{1}=AD_{1}=\frac{\sqrt{5}}{2}
и CM=\frac{\sqrt{3}}{2}
. Следовательно,
\cos\alpha=\cos\angle CE_{1}M=\frac{CE_{1}^{2}+ME_{1}^{2}-CM^{2}}{2CE_{1}\cdot ME_{1}}=\frac{\frac{5}{4}+\frac{5}{4}-\frac{3}{4}}{2\cdot\frac{\sqrt{5}}{2}\cdot\frac{\sqrt{5}}{2}}=\frac{7}{10}.
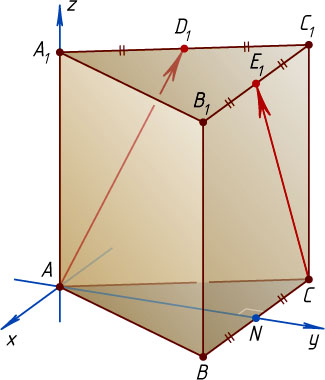
Второй способ. Выберем прямоугольную систему координат следующим образом: поместим начало координат в точку A
, ось Ox
направим по лучу, противоположно направленному с лучом BC
, ось Oy
— по лучу AN
(N
— середина BC
), ось Oz
— по лучу AA_{1}
. Найдём в этой системе координат координаты точек и векторов:
A(0;0;0),~C\left(-\frac{1}{2};\frac{\sqrt{3}}{2};0\right),~D_{1}\left(-\frac{1}{4};\frac{\sqrt{3}}{4};1\right),~E_{1}\left(0;\frac{\sqrt{3}}{2};1\right),
\overrightarrow{AD_{1}}=\left(-\frac{1}{4};\frac{\sqrt{3}}{4};1\right),~\overrightarrow{CE_{1}}=\left(\frac{1}{2};0;1\right).
Тогда
\cos\alpha=\frac{\overrightarrow{AD_{1}}\cdot\overrightarrow{CE_{1}}}{|\overrightarrow{AD_{1}}|\cdot|\overrightarrow{CE_{1}}|}=\frac{-\frac{1}{4}\cdot\frac{1}{2}+\frac{\sqrt{3}}{4}\cdot0+1\cdot1}{\sqrt{\frac{1}{16}+\frac{3}{16}+1}\cdot\sqrt{\frac{1}{4}+1}}=\frac{-\frac{1}{8}+1}{\frac{\sqrt{5}}{2}\cdot\frac{\sqrt{5}}{2}}=\frac{7}{10}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 1.3, с. 5

