7344. В кубе ABCDA_{1}B_{1}C_{1}D_{1}
найдите тангенс угла между плоскостями ADD_{1}
и BDC_{1}
.
Ответ. \sqrt{2}
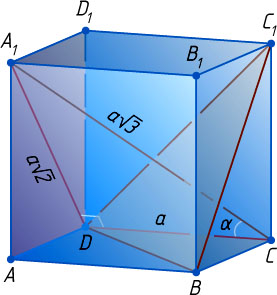
Решение. Первый способ. Пусть ребро куба равно a
. Тогда диагональ грани куба равна a\sqrt{2}
, а диагональ куба равна a\sqrt{3}
.
По теореме о трёх перпендикулярах диагональ CA_{1}
куба перпендикулярна диагонали BD
грани куба, так как ортогональная проекция AC
прямой CA_{1}
на плоскость ABCD
перпендикулярна прямой BD
, лежащей в этой плоскости. Аналогично CA_{1}\perp BC_{1}
. По признаку перпендикулярности прямой и плоскости, прямая CA_{1}
перпендикулярна плоскости BDC_{1}
.
Прямая CD
перпендикулярна плоскости ADD_{1}
, а прямая CA_{1}
перпендикулярна плоскости BDC_{1}
. Угол между плоскостями равен углу между прямыми, соответственно перпендикулярными этим плоскостям, значит, искомый угол \alpha
— это угол DCA_{1}
.
Из прямоугольного треугольника CDA_{1}
находим, что
\tg\alpha=\tg\angle DCA_{1}=\frac{DA_{1}}{CD}=\frac{a\sqrt{2}}{a}=\sqrt{2}.
Второй способ. Плоскость ADD_{1}
параллельна плоскости BCC_{1}
, поэтому искомый угол \alpha
равен углу между плоскостями BCC_{1}
и BDC_{1}
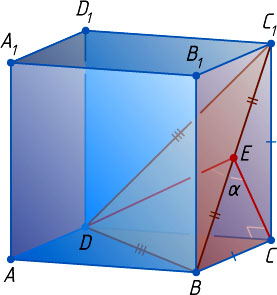
. Пусть E
— середина отрезка BC_{1}
. Тогда прямые CE
и DE
перпендикулярны прямой BC_{1}
и, следовательно, угол CED
— линейный угол двугранного угла, образованного плоскостями BCC_{1}
и BDC_{1}
. Из прямоугольного треугольника CED
находим, что
\tg\alpha=\tg\angle CED=\frac{CD}{EC}=\frac{a}{\frac{a\sqrt{2}}{2}}=\sqrt{2}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 3.2, с. 7

