7346. В единичном кубе ABCDA_{1}B_{1}C_{1}D_{1}
найдите расстояние от точки A
до прямой BD_{1}
.
Ответ. \frac{\sqrt{6}}{3}
.
Решение. Опустим перпендикуляр AH
из вершины A
куба на его диагональ BD_{1}
. Тогда AH
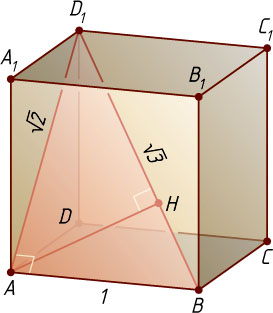
— высота прямоугольного треугольника BAD_{1}
с катетами AB=1
, AD_{1}=\sqrt{2}
и гипотенузой BD_{1}=\sqrt{3}
. Записав двумя способами площадь этого треугольника, получим, что \frac{1}{2}AB\cdot AD_{1}=\frac{1}{2}BD_{1}\cdot AH
, откуда
AH=\frac{AB\cdot AD_{1}}{BD_{1}}=\frac{1\cdot\sqrt{2}}{\sqrt{3}}=\sqrt{\frac{2}{3}}=\frac{\sqrt{6}}{3}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 4.2, с. 8
