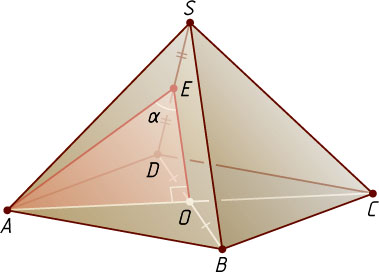
7351. В правильной четырёхугольной пирамиде SABCD
, все рёбра которой равны, точка E
— середина ребра SD
. Найдите тангенс угла между прямыми SB
и AE
.
Ответ. \sqrt{2}
.
Решение. Пусть рёбра пирамиды SABCD
равны a
, O
— центр основания ABCD
. Тогда OE
— средняя линия треугольника SBD
, поэтому OE=\frac{1}{2}SB=\frac{a}{2}
и OE\parallel SB
.
Угол \alpha
между скрещивающимися прямыми SB
и AE
равен углу между пересекающимися прямыми OE
и AE
(так как OE\parallel SB
). По теореме о трёх перпендикулярах OE\perp OA
. В прямоугольном треугольнике AOE
известны катеты AO=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}
и OE=\frac{a}{2}
. Следовательно,
\tg\alpha=\tg\angle AEO=\frac{AO}{OE}=\frac{\frac{a\sqrt{2}}{2}}{\frac{a}{2}}=\sqrt{2}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 4, с. 15
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — , № 3(г), с. 17
