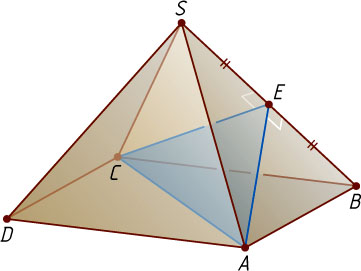
7353. В правильной четырёхугольной пирамиде SABCD
, все рёбра которой равны 1, точка E
— середина ребра SB
. Найдите расстояние от точки B
до плоскости ACE
.
Ответ. \frac{1}{2}
.
Решение. Отрезки AE
и CE
— медианы, а, значит, и высоты равносторонних треугольников ABS
и CBS
, поэтому SB\perp AE
и SB\perp CE
. По признаку перпендикулярности прямой и плоскости прямая SB
перпендикулярна плоскости ACE
, поэтому расстояние от точки B
до этой плоскости равно длине отрезка BE
, т. е. \frac{1}{2}
.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 13, с. 59
