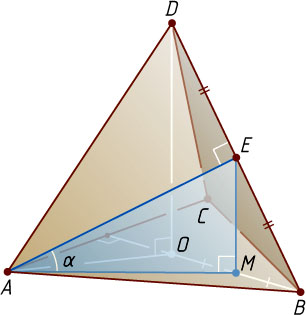
7354. В правильном тетраэдре ABCD
точка E
— середина ребра BD
. Найдите синус угла между прямой AE
и плоскостью ABC
.
Ответ. \frac{\sqrt{2}}{3}
.
Решение. Пусть рёбра тетраэдра равны a
, M
— проекция точки E
на плоскость основания ABC
, O
— центр равностороннего треугольника ABC
. Тогда M
— середина отрезка OB
, а так как AM
— ортогональная проекция наклонной AE
на плоскость ABC
, то угол \alpha
между прямой AE
и плоскостью ABC
— это угол MAE
.
В прямоугольном треугольнике AOD
известно, что
AO=\frac{2}{3}\cdot\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3},~DO=\sqrt{AD^{2}-AO^{2}}=\sqrt{a^{2}-\frac{a^{2}}{3}}=a\sqrt{\frac{2}{3}},
а так как EM
— средняя линия треугольника BOD
, то EM=\frac{1}{2}DO=\frac{1}{2}\sqrt{\frac{2}{3}}
. Из прямоугольного треугольника MAE
находим, что
\sin\alpha=\sin\angle MAE=\frac{EM}{AE}=\frac{\frac{1}{2}\sqrt{\frac{2}{3}}}{\frac{a\sqrt{3}}{2}}=\frac{\sqrt{2}}{3}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 3, с. 19
