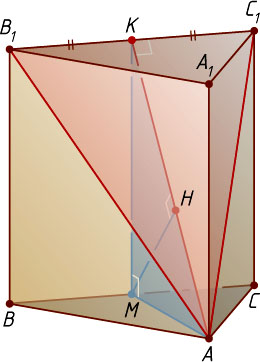
7355. В правильной треугольной призме ABCA_{1}B_{1}C_{1}
, все рёбра которой равны 1, найдите расстояние от точки B
до плоскости AB_{1}C_{1}
.
Ответ. \sqrt{\frac{3}{7}}
.
Решение. Первый способ. Прямая BC
параллельна плоскости AB_{1}C_{1}
, так как она параллельна прямой B_{1}C_{1}
, лежащей в этой плоскости, значит, расстояние от точки B
до плоскости AB_{1}C_{1}
равно расстоянию до неё от любой точки прямой BC
, например, от точки M
— середины ребра BC
.
Опустим перпендикуляр MH
из точки M
на медиану AK
треугольника AB_{1}C_{1}
. Прямая MH
лежит в плоскости AKM
, перпендикулярной прямой B_{1}C_{1}
, значит, MH\perp B_{1}C_{1}
. Таким образом, прямая MH
перпендикулярна двум пересекающимся прямым AK
и B_{1}C_{1}
плоскости AB_{1}C_{1}
. Следовательно, MH
— перпендикуляр к плоскости AB_{1}C_{1}
, а искомое расстояние от точки B
до плоскости AB_{1}C_{1}
равно длине отрезка MH
.
В прямоугольном треугольнике AMK
известно, что
MK=BB_{1}=1,~AM=\frac{AB\sqrt{3}}{2}=\frac{\sqrt{3}}{2},~AK=\sqrt{MK^{2}+AM^{2}}=\sqrt{1+\frac{3}{4}}=\frac{\sqrt{7}}{2}.
Записав двумя способами площадь треугольника AMK
получим, что \frac{1}{2}AK\cdot MH=\frac{1}{2}AM\cdot MK
, откуда
MH=\frac{AM\cdot MK}{AK}=\frac{\frac{\sqrt{3}}{2}\cdot1}{\frac{\sqrt{7}}{2}}=\sqrt{\frac{3}{7}}.
Второй способ. Пусть K
— середина ребра B_{1}C_{1}
, а искомое расстояние равно d
. Применим метод объёмов.
V_{ABCA_{1}B_{1}C_{1}}=S_{\triangle ABC}\cdot AA_{1}=\frac{\sqrt{3}}{4}\cdot1=\frac{\sqrt{3}}{4}.
Объём тетраэдра ABB_{1}C_{1}
равен разности объёмов призмы ABCA_{1}B_{1}C_{1}
и тетраэдров AA_{1}B_{1}C_{1}
и ABCC_{1}
, т. е.
V_{ABB_{1}C_{1}}=V_{ABCA_{1}B_{1}C_{1}}-\frac{1}{3}V_{ABCA_{1}B_{1}C_{1}}-\frac{1}{3}V_{ABCA_{1}B_{1}C_{1}}=\frac{1}{3}V_{ABCA_{1}B_{1}C_{1}}=\frac{1}{3}\cdot\frac{\sqrt{3}}{4}=\frac{\sqrt{3}}{12}.
С другой стороны,
V_{ABB_{1}C_{1}}=\frac{1}{3}S_{\triangle AB_{1}C_{1}}\cdot d=\frac{1}{3}\cdot\frac{1}{2}B_{1}C_{1}\cdot AK\cdot d=\frac{1}{3}\cdot\frac{1}{2}\cdot1\cdot\frac{\sqrt{7}}{2}\cdot d=\frac{d\sqrt{7}}{12}.
Из равенства \frac{d\sqrt{7}}{12}=\frac{\sqrt{3}}{12}
находим, что d=\sqrt{\frac{3}{7}}
.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 14, с. 59

