7358. В кубе ABCDA_{1}B_{1}C_{1}D_{1}
найдите косинус угла между плоскостями BA_{1}C_{1}
и AB_{1}D_{1}
.
Ответ. \frac{1}{3}
.
Решение. Диагональ DB_{1}
куба ABCDA_{1}B_{1}C_{1}D_{1}
перпендикулярна плоскости BA_{1}C_{1}
, так как она перпендикулярна двум пересекающимся прямым A_{1}C_{1}
и BC_{1}
этой плоскости (по теореме о трёх перпендикулярах). Аналогично диагональ CA_{1}
перпендикулярна плоскости AB_{1}D_{1}
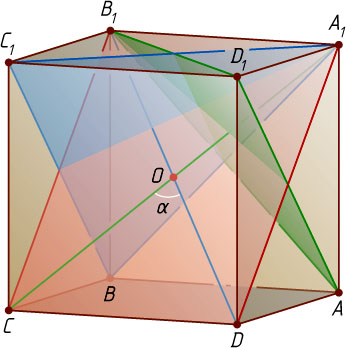
. Следовательно, угол \alpha
между плоскостями BA_{1}C_{1}
и AB_{1}D_{1}
равен углу между прямыми DB_{1}
и CA_{1}
, соответственно перпендикулярными этим плоскостям.
Рассмотрим сечение CDD_{1}C_{1}
. Диагонали прямоугольника CDD_{1}C_{1}
равны и делятся точкой O
пересечения пополам. Пусть ребро куба равно a
. Тогда
OC=OD=\frac{1}{2}DB_{1}=\frac{1}{2}\cdot a\sqrt{3}=\frac{a\sqrt{3}}{2}.
По теореме косинусов
\cos\alpha=\cos\angle COD=\frac{OC^{2}+OD^{2}-CD^{2}}{2OC\cdot OD}=\frac{\frac{3}{4}a^{2}+\frac{3}{4}a^{2}-a^{2}}{2\cdot\frac{a\sqrt{3}}{2}\cdot\frac{a\sqrt{3}}{2}}=\frac{1}{3}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 2, с. 24
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 1(в), с. 26
Источник: Мерзляк А. Г., Номировский В. М., Поляков В. М. Геометрия. 10 класс. Углублённый уровень. — М.: Вентана-Граф, 2019. — № 14.49, с. 165
