7359. В кубе ABCDA_{1}B_{1}C_{1}D_{1}
найдите косинус угла между плоскостями AB_{1}D_{1}
и CB_{1}D_{1}
.
Ответ. \frac{1}{3}
.
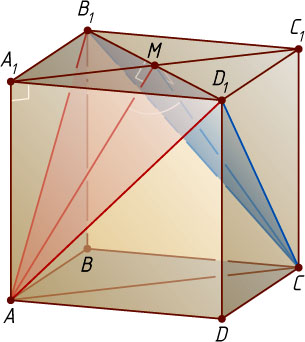
Решение. Первый способ. Пусть ребро куба равно a
, M
— центр грани A_{1}B_{1}C_{1}D_{1}
. Тогда AM
и CM
— высоты равнобедренных треугольников AB_{1}D_{1}
и CB_{1}D_{1}
, поэтому AMC
— линейный угол искомого двугранного угла.
Пусть ребро куба равно a
. Из прямоугольного треугольника AA_{1}M
находим, что
AM=\sqrt{AA_{1}^{2}+A_{1}M^{2}}=\sqrt{a^{2}+\left(\frac{a\sqrt{2}}{2}\right)^{2}}=\sqrt{a^{2}+\frac{a^{2}}{2}}=a\sqrt{\frac{3}{2}}.
Аналогично CM=a\sqrt{\frac{3}{2}}
. По теореме косинусов
\cos\angle AMC=\frac{AM^{2}+CM^{2}-AC^{2}}{2AM\cdot CM}=\frac{\frac{3a^{2}}{2}+\frac{3a^{2}}{2}-2a^{2}}{2\cdot a\sqrt{\frac{3}{2}}\cdot a\sqrt{\frac{3}{2}}}=\frac{1}{3}.
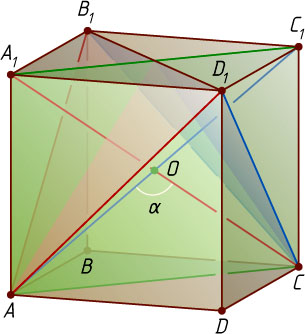
Второй способ. Диагональ CA_{1}
куба ABCDA_{1}B_{1}C_{1}D_{1}
перпендикулярна плоскости AB_{1}D_{1}
, так как она перпендикулярна двум пересекающимся прямым B_{1}D_{1}
и AB_{1}
этой плоскости (по теореме о трёх перпендикулярах). Аналогично диагональ AC_{1}
перпендикулярна плоскости CB_{1}D_{1}
. Следовательно, угол \alpha
между плоскостями AB_{1}D_{1}
и CB_{1}D_{1}
равен углу между прямыми CA_{1}
и AC_{1}
, соответственно перпендикулярными этим плоскостям.
Рассмотрим сечение AA_{1}C_{1}C
. Диагонали прямоугольника AA_{1}C_{1}C
равны и делятся точкой O
пересечения пополам. Пусть ребро куба равно a
. Тогда
OC=OD=\frac{1}{2}AC_{1}=\frac{1}{2}\cdot a\sqrt{3}=\frac{a\sqrt{3}}{2}.
По теореме косинусов
\cos\alpha=\cos\angle AOC=\frac{OA^{2}+OC^{2}-AC^{2}}{2OA\cdot OC}=\frac{\frac{3}{4}a^{2}+\frac{3}{4}a^{2}-2a^{2}}{2\cdot\frac{a\sqrt{3}}{2}\cdot\frac{a\sqrt{3}}{2}}=-\frac{1}{3},
а так как угол между плоскостями не может быть тупым, то косинус искомого угла равен \frac{1}{3}
.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 9, с. 45

