7360. В правильной треугольной призме ABCA_{1}B_{1}C_{1}
, все рёбра которой равны, найдите косинус угла между прямыми AB_{1}
и BC_{1}
.
Ответ. \frac{1}{4}
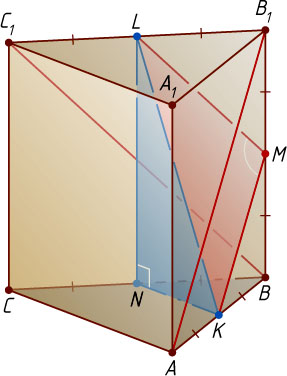
Решение. Пусть все рёбра призмы равны a
, а точки K
, L
, M
и N
— середины рёбер AB
, B_{1}C_{1}
, BB_{1}
и BC
соответственно. Тогда KN
, KM
и ML
— средние линии треугольников ABC
, ABB_{1}
и BB_{1}C_{1}
,
LM=KM=\frac{1}{2}AB_{1}=\frac{a\sqrt{2}}{2},~KN=\frac{1}{2}AC=\frac{a}{2},~AB_{1}\parallel KM,~BC_{1}\parallel ML.
Искомый угол \alpha
между прямыми AB_{1}
и BC_{1}
равен углу между соответственно параллельными им прямыми KM
и ML
.
Из прямоугольного треугольника KLN
находим, что
KL^{2}=KN^{2}+LN^{2}=\frac{a^{2}}{4}+a^{2}=\frac{5}{4}a^{2}.
По теореме косинусов
\cos\angle KML=\frac{KM^{2}+ML^{2}-KL^{2}}{2KM\cdot ML}=\frac{\frac{a^{2}}{2}+\frac{a^{2}}{2}-\frac{5a^{2}}{4}}{2\cdot\frac{a\sqrt{2}}{2}\cdot\frac{a\sqrt{2}}{2}}=-\frac{1}{4}.
Следовательно, \cos\alpha=\frac{1}{4}
.
