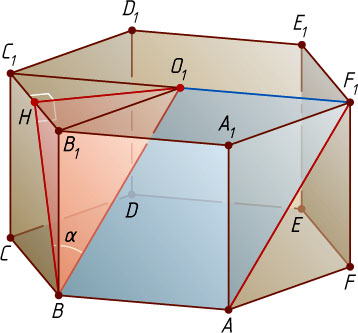
7362. В правильной шестиугольной призме ABCDEFA_{1}B_{1}C_{1}D_{1}E_{1}F_{1}
, все рёбра которой равны, найдите синус угла между прямой AF_{1}
и плоскостью BCC_{1}
.
Ответ. \frac{\sqrt{6}}{4}
.
Решение. Пусть все рёбра данной призмы равны a
, O_{1}
— центр правильного шестиугольника A_{1}B_{1}C_{1}D_{1}E_{1}F_{1}
, H
— середина ребра B_{1}C_{1}
. Противоположные стороны AB
и O_{1}F_{1}
четырёхугольника ABO_{1}F_{1}
равны и параллельны, значит, ABO_{1}F_{1}
— параллелограмм. Следовательно, BO_{1}=AF_{1}
и BO_{1}\parallel AF_{1}
, поэтому угол \alpha
между прямой AF_{1}
и плоскостью BCC_{1}
равен углу между прямой BO_{1}
и этой плоскостью.
Прямая O_{1}H
перпендикулярна двум пересекающимся прямым B_{1}C_{1}
и BB_{1}
плоскости BCC_{1}B_{1}
, поэтому O_{1}H
— перпендикуляр к этой плоскости. Значит, BH
— ортогональная проекция наклонной O_{1}B
на плоскость BCC_{1}B_{1}
, и угол O_{1}BH
равен искомому. Следовательно,
\sin\alpha=\sin\angle O_{1}BH=\frac{O_{1}H}{BO_{1}}=\frac{O_{1}H}{AF_{1}}=\frac{\frac{a\sqrt{3}}{2}}{a\sqrt{2}}=\frac{\sqrt{3}}{2\sqrt{2}}=\frac{\sqrt{6}}{4}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 6, с. 44
