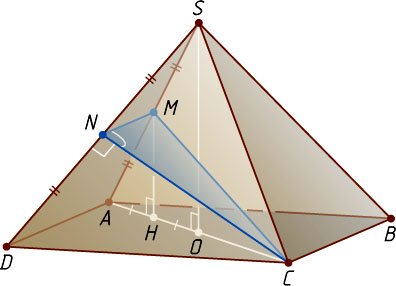
7365. В правильной четырёхугольной пирамиде SABCD
(S
— вершина), все рёбра которой равны, точка N
— середина ребра SD
. Найдите синус угла между прямыми AD
и CN
.
Ответ. \frac{\sqrt{33}}{6}
.
Решение. Пусть каждое ребро пирамиды SABCD
равно a
, O
— центр основания ABCD
, H
— основание перпендикуляра, опущенного из середины M
ребра SA
на плоскость основания. Тогда MN
— средняя линия треугольника SAD
, поэтому MN=\frac{1}{2}AD=\frac{a}{2}
и MN\parallel AD
. Из прямоугольного треугольника AOS
находим, что
SO=\sqrt{SA^{2}-OA^{2}}=\sqrt{a^{2}-\left(\frac{a\sqrt{2}}{2}\right)^{2}}=\frac{a\sqrt{2}}{2},
а так как CN
— высота равностороннего треугольника SCD
, то CN=\frac{a\sqrt{3}}{2}
.
Угол \alpha
между скрещивающимися прямыми AD
и CN
равен углу между пересекающимися прямыми MN
и CN
(так как MN\parallel AD
). Точка H
лежит на отрезке OA
— проекции бокового ребра SA
на плоскость основания пирамиды, причём MH
— средняя линия треугольника AOS
, поэтому
MH=\frac{1}{2}SO=\frac{1}{2}\cdot\frac{a\sqrt{2}}{2}=\frac{a\sqrt{2}}{4},
а так как CH=CO+OH=\frac{a\sqrt{2}}{2}+\frac{a\sqrt{2}}{4}=\frac{3a\sqrt{2}}{4}
, то
CM^{2}=MH^{2}+CH^{2}=\left(\frac{a\sqrt{2}}{4}\right)^{2}+\left(\frac{3a\sqrt{2}}{4}\right)^{2}=\frac{5a^{2}}{4}.
По теореме косинусов из треугольника CNM
находим, что
\cos\angle CNM=\frac{MN^{2}+CN^{2}-CM^{2}}{2MN\cdot CN}=\frac{\frac{a^{2}}{4}+\frac{3a^{2}}{4}-\frac{5a^{2}}{4}}{2\cdot\frac{a}{2}\cdot\frac{a\sqrt{3}}{2}}=-\frac{1}{2\sqrt{3}}.
Следовательно, \cos\alpha=\frac{1}{2\sqrt{3}}
, а
\sin\alpha=\sqrt{1-\cos^{2}\alpha}=\sqrt{1-\frac{1}{12}}=\frac{\sqrt{11}}{2\sqrt{3}}=\frac{\sqrt{33}}{6}.