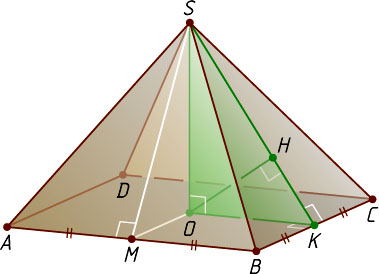
7366. В правильной четырёхугольной пирамиде SABCD
(S
— вершина), все рёбра которой равны, найдите синус угла между прямой SM
и плоскостью BSC
, где M
— середина ребра AB
.
Ответ. \frac{\sqrt{2}}{3}
.
Решение. Пусть O
— центр основания ABCD
, рёбра данной пирамиды равны a
, а искомый угол равен \alpha
. Поскольку MO\parallel BC
, прямая MO
параллельна плоскости BSC
, поэтому расстояние от точки M
до плоскости BSC
равно расстоянию от точки O
до этой плоскости.
Опустим перпендикуляр OH
из точки O
на апофему SK
пирамиды, лежащую в плоскости боковой грани BSC
. Прямая BC
перпендикулярна плоскости SOK
, содержащей прямую OH
, так как BC\perp OK
и BC\perp SK
, поэтому прямая OH
перпендикулярна двум пересекающимся прямым SK
и BC
плоскости SBC
. Следовательно, OH
— перпендикуляр к этой плоскости.
В прямоугольном треугольнике SOK
известно, что
OK=\frac{a}{2},~SO=\sqrt{SB^{2}-OB^{2}}=\sqrt{a^{2}-\left(\frac{a\sqrt{2}}{2}\right)^{2}}=\frac{a\sqrt{2}}{2},~SK=\frac{a\sqrt{3}}{2}.
Записав двумя способами площадь прямоугольного треугольника SOK
, получим равенство \frac{1}{2}SK\cdot OH=\frac{1}{2}OK\cdot SO
, откуда
OH=\frac{OK\cdot SO}{SK}=\frac{\frac{a}{2}\cdot\frac{a\sqrt{2}}{2}}{\frac{a\sqrt{3}}{2}}=\frac{a\sqrt{2}}{2\sqrt{3}}.
Синус искомого угла равен отношению расстояния от точки M
до плоскости SBC
(т. е. длине отрезка OH
) к длине наклонной MS
к этой плоскости. Следовательно,
\sin\alpha=\frac{OH}{MS}=\frac{\frac{a\sqrt{2}}{2\sqrt{3}}}{\frac{a\sqrt{3}}{2}}=\frac{\sqrt{2}}{3}.