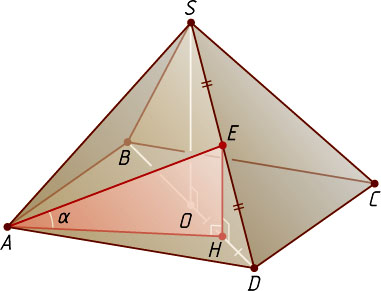
7367. В правильной четырёхугольной пирамиде SABCD
, все рёбра которой равны, точка E
— середина ребра SD
. Найдите синус угла между прямой AE
и плоскостью ABC
.
Ответ. \frac{\sqrt{6}}{6}
.
Решение. Пусть рёбра пирамиды SABCD
равны a
, O
— центр основания ABCD
, H
— проекция точки E
на плоскость основания. Тогда точка H
лежит на отрезке OD
— проекции наклонной SD
на эту плоскость, причём H
— середина OD
. Из прямоугольного треугольника SOD
находим, что
SO=\sqrt{SD^{2}-OD^{2}}=\sqrt{a^{2}-\left(\frac{a\sqrt{2}}{2}\right)^{2}}=\frac{a\sqrt{2}}{2},
а так как EH
— средняя линия треугольника SOD
, то EH=\frac{1}{2}SO=\frac{a\sqrt{2}}{4}
. Отрезок AE
— медиана, а значит, и высота равностороннего треугольника ADS
со стороной a
, поэтому AE=\frac{a\sqrt{3}}{2}
.
Угол \alpha
между прямой AE
и плоскостью ABCD
— это угол между прямой AE
и её ортогональной проекцией AH
на плоскость ABCD
, т. е. угол EAH
. Из прямоугольного треугольника AHE
находим, что
\sin\alpha=\sin\angle EAH=\frac{EH}{AE}=\frac{\frac{a\sqrt{2}}{4}}{\frac{a\sqrt{3}}{2}}=\frac{\sqrt{2}}{2\sqrt{3}}=\frac{\sqrt{6}}{6}.