7368. Найдите синус угла между диагональю основания и боковой гранью правильной четырёхугольной пирамиды, все рёбра которой равны между собой.
Ответ. \frac{1}{\sqrt{3}}
.
Решение. Пусть все рёбра правильной четырёхугольной пирамиды SABCD
с вершиной S
равны a
. Обозначим через \alpha
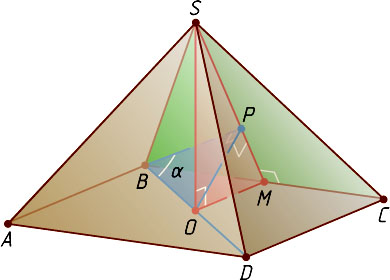
искомый угол между диагональю BD
основания и плоскостью боковой грани SBC
.
Пусть M
— середина BC
; O
— центр квадрата ABCD
, тогда SO
— высота пирамиды. В прямоугольном треугольнике SOM
опустим высоту OP
. Поскольку SM\perp BC
и OM\perp BC
, то по теореме о трёх перпендикулярах OP\perp BC
. Значит, OP
— перпендикуляр к плоскости SBC
, а \angle PBO=\alpha
. Следовательно,
\sin\alpha=\sin\angle PBO=\frac{OP}{OB}.
Из равностороннего треугольника SBC
и прямоугольного треугольника SOM
находим, что
SM=\frac{a\sqrt{3}}{2},~SO=\sqrt{SM^2-OM^2}=\sqrt{\frac{3a^2}{4}-\frac{a^2}{4}}=\frac{a\sqrt{2}}{2},
а так как SM\cdot OP=SO\cdot OM
, то
OP=\frac{SO\cdot OM}{SM}=\frac{\frac{a\sqrt{2}}{2}\cdot\frac{a}{2}}{\frac{a\sqrt{3}}{2}}=\frac{a}{\sqrt{6}}.
Следовательно,
\sin\alpha=\frac{OP}{OB}=\frac{\frac{a}{\sqrt{6}}}{\frac{a}{\sqrt{2}}}=\frac{1}{\sqrt{3}}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 5, с. 20
