7372. В правильной шестиугольной пирамиде SABCDEF
с основанием ABCDEF
найдите косинус угла между плоскостями SAF
и SBC
, если известно, что стороны основания равны 1, а боковые рёбра равны 2.
Ответ. \frac{1}{5}
.
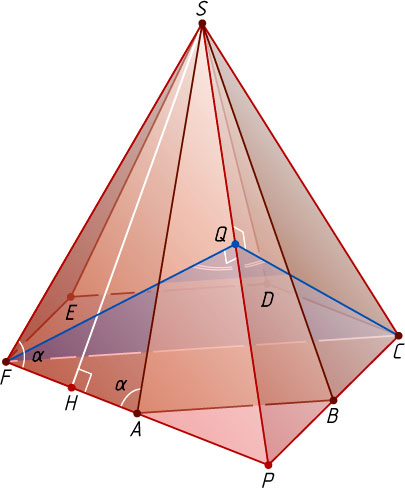
Решение. Пусть P
— точка пересечения продолжений отрезков AF
и BC
. Точки P
и S
— общие точки плоскостей SAF
и SBC
, значит, эти плоскости пересекаются по прямой SP
.
Треугольники SFP
и CSP
равны, поэтому их высоты, опущенные на общую сторону SP
, проходят через одну и ту же точку Q
. Следовательно, CQF
— линейный угол двугранного угла, образованного плоскостями SAF
и SBC
.
Углы при вершинах A
и B
треугольника APB
равны 60^{\circ}
, поэтому BP=AP=AB=1
. Пусть SH
— высота треугольника SAF
, а \angle SAF=\angle SFA=\alpha
. Тогда
SH=\sqrt{SA^{2}-AF^{2}}=\sqrt{4-\frac{1}{4}}=\frac{\sqrt{15}}{2},~\cos\alpha=\frac{AH}{SA}=\frac{\frac{1}{2}}{2}=\frac{1}{4},
SP=\sqrt{SF^{2}+FP^{2}-2SF\cdot FP\cos\alpha}=\sqrt{4+4-2\cdot2\cdot2\cdot\frac{1}{4}}=\sqrt{6}.
Записав двумя способами площадь треугольника SFP
, получим равенство \frac{1}{2}SP\cdot FQ=\frac{1}{2}FP\cdot SH
, откуда
FQ=\frac{2\cdot\frac{\sqrt{15}}{2}}{\sqrt{6}}=\sqrt{\frac{5}{2}}.
Следовательно,
\cos\angle CQF=\frac{FQ^{2}+CQ^{2}-CF^{2}}{2FQ\cdot CQ}=\frac{\frac{5}{2}+\frac{5}{2}-4}{2\cdot\sqrt{\frac{5}{2}}\cdot\sqrt{\frac{5}{2}}}=\frac{1}{5}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 7, с. 26
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6(б), с. 26
