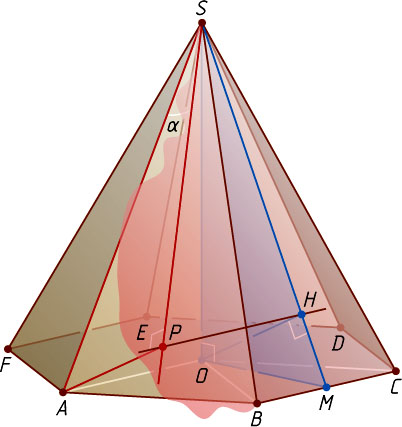
7373. В правильной шестиугольной пирамиде SABCDEF
с основанием ABCDEF
найдите косинус угла между прямой SA
и плоскостью SBC
, если известно, что стороны основания равны 1, а боковые рёбра равны 2.
Ответ. \frac{1}{2}\sqrt{\frac{3}{5}}
.
Решение. Пусть O
— центр правильного шестиугольника ABCDEF
, P
— ортогональная проекция точки A
на плоскость SBC
. Тогда SP
— ортогональная проекция наклонной AS
на эту плоскость, а косинус искомого угла \alpha
равен отношению \frac{AP}{SA}
.
Поскольку OA\parallel BC
, прямая OA
параллельна плоскости BSC
, поэтому расстояние AP
от точки A
до плоскости BSC
равно расстоянию от точки O
до этой плоскости.
Опустим перпендикуляр OH
из точки O
на апофему SM
, лежащую в грани SBC
. Прямая BC
перпендикулярна двум пересекающимся прямым OM
и SM
плоскости SOM
, значит, прямая BC
перпендикулярна прямой OH
, лежащей в этой плоскости. Таким образом, прямая OH
перпендикулярна двум пересекающимся прямым BC
и SM
плоскости SBC
. Следовательно, OM
— перпендикуляр к плоскости SBC
, и AH=SM
.
Из прямоугольных треугольников SBM
и SOB
находим, что
SM=\sqrt{SB^{2}-BM^{2}}=\sqrt{4-\frac{1}{4}}=\frac{\sqrt{15}}{2},~SO=\sqrt{SB^{2}-OB^{2}}=\sqrt{4-1}=\sqrt{3},
а так как OM
— высота равностороннего треугольника BOC
, то
OM=\frac{BC\sqrt{3}}{2}=\frac{\sqrt{3}}{2}.
Записав двумя способами площадь прямоугольного треугольника SOM
, получим равенство \frac{1}{2}SM\cdot OH=\frac{1}{2}OM\cdot SO
, откуда
OH=\frac{OM\cdot SO}{SM}=\frac{\frac{\sqrt{3}}{2}\cdot\sqrt{3}}{\frac{\sqrt{15}}{2}}=\frac{\sqrt{3}}{\sqrt{5}}.
Следовательно,
\cos\alpha=\frac{AP}{SA}=\frac{OH}{SA}=\frac{\frac{\sqrt{3}}{\sqrt{5}}}{2}=\frac{1}{2}\sqrt{\frac{3}{5}}.
Источник: Смирнов В. А. ЕГЭ 2010. Математика. Задача C2. Геометрия. Стереометрия / Под. ред. А. Л. Семёнова, И. В. Ященко. — М.: МЦНМО, 2010. — № 5, с. 56
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 6(в), с. 45
